本文是关于论文《Range-based Obstructed Nearest Neighbor Queries(RONN)》(基于范围的有障碍最近邻查询)的阅读笔记。没有完全读懂。
一、记号
RONN:基于范围的有障碍最近邻(range-based obstructed nearest neighbor)
CONN:连续有障碍最近邻(continuous obstructed nearest neighbor)
CONNB:CONN-based算法(作为baseline)
RONN-RF:通过R树过滤的RONN(RONN by R-tree Filtering)
O-tree:O树,将有障碍空间划分为多个非有障碍空间,在RONN中快速检索高质量的候选对象
OOB:最优有障碍平衡(optimal obstacle balance),空间划分的方案
RONN-OA:通过O树加速的RONN(RONN by O-tree Acceleration)
RNN:范围最近邻
二、背景
RNN查询是检索某个空间区域的最近邻,是一种基础查询,可以归类为以下四个使用场景:
- 隐私保护:用户不愿意暴露自己确切的位置信息,空间匿位(Spatial cloaking)技术,模糊用户在空间区域的确切位置
- 连续查询:当用户正在移动时的连续查询时,在服务器上处理单个NN查询是低效的,提交一个RNN查询来预取这个区域的所有可能的近邻作为候选集是一个更好的选择
- 批处理:相近的最近邻查询可能是由不同用户发出的,将空间上邻近的最近邻查询分成一组,并将其批处理,并从返回的候选集中解析每个NN查询的结果。
- 位置不确定性:由于定位技术、网络延迟等带来的限制,用户的位置的不确定性仍是一个问题。可以给RNN查询设定一个空间区域(用户在该区域内)。
之前的RNN工作都是假设是一个平坦的,没有障碍的空间,并使用欧几里得距离和数据对象和查询范围之间的最短距离,来作为距离的度量标准。但在现实中,两个点之间可能有障碍,所以就要使用有障碍距离,即两个点之间没有任何障碍的最短路径。
三、文章概述
1. 简短概述
RONN是CONN的进阶版,为了解决RONN,首先提出了CONNB作为baseline,它将一个RONN查询划分为一个范围查询和四个CONN查询。为了克服CONNB查询次数太多的问题,又提出了RONN-RF算法,它和CONNB一样都是基于R树的。但是R树本身也有缺点,所以又提出了O树来代替R树,O树将有阻碍空间划分为无阻碍空间并进行检索。同时还提出了构建O树的算法和空间划分方案OOB(最优障碍平衡)。有了O树,又在其基础上提出了RONN-OA算法,它利用O树来加速RONN查询的处理。
2. 详细概述
本文提出了CONNB作为baseline,它将RONN查询简化为了一个范围查询和四个CONN查询。(R树保存数据对象和障碍)本文是第一个试图解决RONN问题的文章。
为了解决CONNB的缺点,又提出了RONN-RF算法,它采用高效的过滤策略来促进查询的效率。然而,在处理RONN时,由于障碍在R树中的表示问题,存在两个困难:
- 对于RONN-RF和CONNB都需要多次遍历R树,前者需要遍历两次,后者需要遍历5次
- R-树索引同一欧氏空间中的数据对象和障碍物,增加了计算量
为了解决以上两个问题,又提出了O-tree,它在无障碍子空间里组织数据对象和障碍物。他的主要思想是将障碍空间划分为无障碍子空间。R树最终被嵌入到O树中用来解决无障碍子空间。
为了建立平衡的O树,提出了树的平衡的概念——障碍平衡(obstacle balance)。因为O树的平衡主要受选择障碍物的顺序的影响。所以提出了一种空间划分方案——OOB(optimal obstacle balance)。此外,提出了RONN-OA的算法来加速RONN的查询过程。
文章最后在真实数据和合成数据上进行了实验,验证了RONN-OA和RONN-RF都比CONNB提升很多。
四、定义
RONN查询:给定一个数据对象的集合 P 和障碍的集合 O,一个带有查询范围 R 的 RONN 查询,基于有障碍距离,检索 R 中所有点的最近邻,即$RONN(Q)={ONN(p)|p\in R}$。
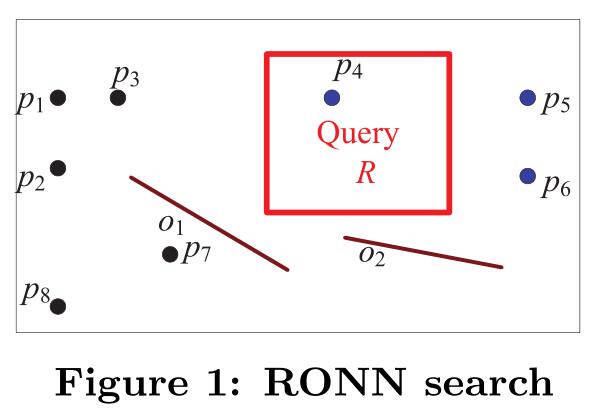
如图一所示,圆点表示数据对象,红线段表示障碍物,矩形表示查询范围,蓝色点表示查询结果。p7不在结果集中,因为有障碍物o1,p3不在结果集中,因为p4比它更近。在处理RONN时的主要挑战是采用什么样的障碍距离作为度量标准。
无障碍路径(obstacle-free path):$P(p,p’)=<d_0,d_1,…,d_n>$,其中$d_i$是空间中的点,$d_0=p,d_n=p’$。
有障碍距离(obstructed distance):无障碍路径$P(p,p’)$的距离定义为$|P(p,p’)|=\Sigma_{i\in[0,n-1]}dist(d_i,d_{i+1})$,其中$dist(d_i,d_{i+1})$是两点间的欧几里得距离。点$p$和$p’$之间的有障碍距离表示为$||p,p’||$,它是最短的无障碍路径的距离。
有障碍最近邻(obstructed nearest neighbor):查询点$p$是点$q$的ONN当且仅当$\forall p’\in P-p,||p,q||\leq||p’,q||$,即$p$到$q$的有障碍距离小于等于其他点到$q$的有障碍距离。
连续有障碍最近邻(continuous obstructed nearest neighbor):查询线段$\bar{q}$的CONN记作$CONN(\bar{q})$,满足$\forall q\in\bar{q},ONN(q)\in CONN(\bar{q})$,即线段上所有点的ONN的集合。
CONN的分割点(split points for CONN):我们用$\bar{ab}$来表示查询线段$\bar{q}$,其中$a$和$b$是线段的两个端点,$\bar{q}$由$\bar{q_1},\bar{q_2},…,\bar{q_t}$组成,其中$\bar{q_1}=\bar{as_1},\bar{q_2}=\bar{s_1s_2},…,\bar{q_{t-1}}=\bar{s_{t-1}b}$。那么称$s_1,s_2,…,s_{t-1}$是线段$\bar{q}$的分割点。
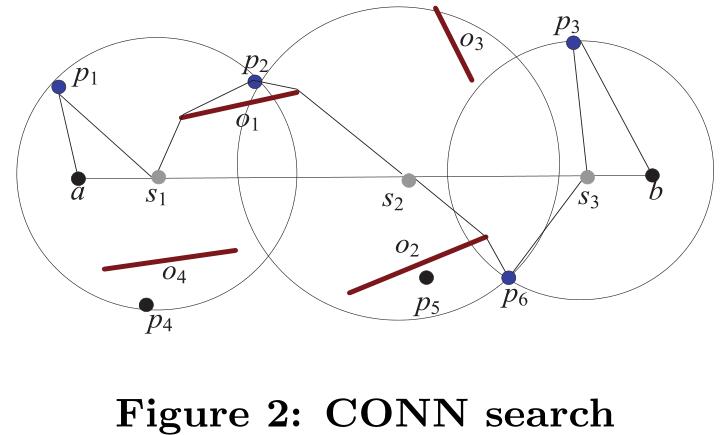
如图二所示,$\bar{ab}$是查询线段,CONN的输出是${<p_1,\bar{as_1}>,<p_2,\bar{s_1s_2}>,<p_6,\bar{s_2,s_3}>,<p_3,\bar{s_3b}>}$,其中$s_1,s_2,s_3$是分割点。(个人感觉$s_1,s_3$的位置可能不止一个)
五、CONNB算法
给定一个具有查询范围R的RONN查询Q,任何在R内部的对象都是查询的一个RONN,所以可以先找到在R内部的所有RONN,然后再找在R外部的RONN,R外部的RONN是R的边界的ONN的集合。
引理1:对象p是R外部的一个RONN当且仅当p在R的外部,并且p至少是R的边界上一点的ONN。
根据引理1,一个RONN查询可以分为5个查询:四个CONN查询(R的每一边作为一个查询线段)和一个范围查询。在CONNB中,R树被作用索引数据对象和障碍物。
六、RONN-RF
注意,在查询处理期间获得的一些中间RONN可能会取消位于远离查询范围R的某些RONN候选资格。所以,一个有效的过滤方法是使用距离浏览方法(distance browing approach),根据RONN到R的最小欧氏距离来获得RONN。所以又提出了RONN-RF算法,它建立在R树上,便于基于距离的浏览和过滤。
RONN集合到线段的最大有障碍距离(maximum obstructed distance of an RONN set to line segment):给定一个中间RONN的集合P和线段$\bar{ab}$,称$||m,p_m||$是从P到$\bar{ab}$的最大有障碍距离,表示为$max_odis(P,\bar{ab})$,当且仅当线段$\bar{ab}$上存在一个点m使得,$\forall\text{ point i on }\bar{ab},\quad ||i,ONN_P(i)||\leq||m,ONN_P(p)||$,$ONN_P(i)$表示在集合P中i点的ONN。(小写的p是什么,文章中没有提到)
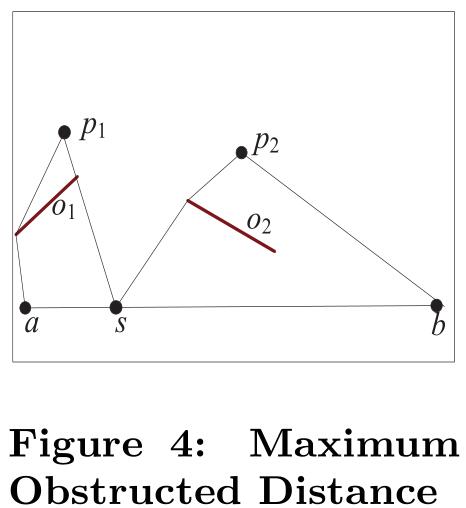
如图4所示,$p_1$和$p_2$分别是在线段$\bar{as}$和$\bar{sb}$上所有点的RONN,$max_odist(p_1,\bar{as})=||p_1,s||\leq||p_2,b||=max_odist(p_2,\bar{sb})$,即$max_odis(P,\bar{ab})$
每个边的MOD(maximum obstructed distances)用来过滤掉不合格的对象。
RONN-RF首先通过范围查询来获取内部RONN,并用其来初始化四个MOD,然后遍历R树,按到查询范围R的最小欧几里德距离的升序访问数据对象,以确定它们是否是每个边的ONN。在遍历R树时,使用堆H来存储R树条目,包括MBB(minimum bounding boxes)、数据对象和障碍物。
初始化时,H只有根节点条目e,RONN-RF通过到R的最短距离对条目e进行弹出,检查从e到R的最小欧几里德距离是否大于所有当前MOD,如果大于,则e将被删除,并且一个新条目将被弹出。否则,如果e是MBB(即内部索引节点),则将其所有子项推送到H中进行进一步处理。另一方面,如果e是R-树的叶节点,则有两种情况:
- e是障碍物:它被插入到可视化图VG中,用于计算边上分裂点;
- e是一个数据对象:它通过在范围边界的边上寻找分割点(FindSP)来更新RONN结果和对应于每个边的MOD(稍后将进一步讨论)。
重复上述查询处理步骤(即从手上清除新条目的堆等),直到H变为空。
RONN-RF同时测试一个数据对象到所有边的情况,而不是对每个边依次处理,这样提升了速度。RONN-RF只需要遍历R-树一次而不是四次。让$r_i,i=1,2,3,4$是查询范围R的角点,$\bar{E_{ij}}$表示边$\bar{r_ir_j}$,给定中间RONN的结果集($RS_{ij}$)以及已访问过的障碍物的可视化图VG,我们就能确定数据对象在测试p下是否是边$\bar{E_{ij}}$的RONN。如果是,那么我们就可以获得分割点的列表,它可以把$\bar{E_{ij}}$分割成和$RS_{ij}$中的RONN相关的线段。此外,$\bar{E_{ij}}$的MOD也会被更新。
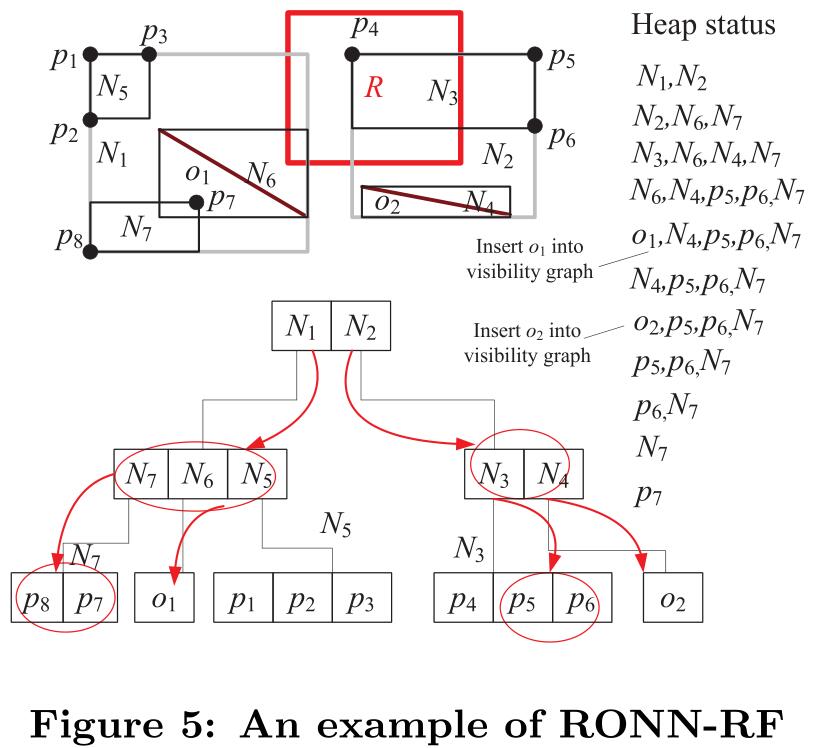
给定一个查询范围R,RONN-RF首先发出一个范围查询来获得内部的RONN,即$p_4$,并用其初始化四个边的MOD。接着,通过遍历R树来得到外部的RONN。一开始,堆中只有$N_1,N_2$,按它们到R的欧几里得距离进行升序排序。从H弹出顶部的$N_1$,由于$N_1$是内部节点,需要比较它的子条目$N_5,N_6,N_7$到R的欧几里得距离和已有的MOD的关系,并将$N_6,N_7$插入回堆中,而$N_5$由于大于MOD而被过滤掉了。类似的将$N_2$弹出,其子条目$N_3,N_4$入堆;然后$N_3$出堆,$p_5,p_6$被插入到H中,$p_4$已经在RONN的结果集中了,所以不再插入;弹出$N_6$,把其子条目$o_1$插入到可视化图VG中;同理,弹出$N_4$,在VG中插入$o_2$;然后将$p_5$弹出,因为它是数据对象,并且是一个RONN,通过VG更新分割点和每条边的MOD;同理$p_6$包含在结果集中;最后将$N_7$弹出,将其子条目$p_7$插入到H中,因为$p_8$的距离大于某些MOD,所以不插入。然后弹出 $p_7$,但由于$o_1$的存在,不能更新当前RONN结果,此时H为空,RONN结果集包含$p_4,p_5,p_6$。
在以上样例中,每条边都保存一个MOD,一个RONN的候选对象被过滤掉当且仅当它到查询范围边界的欧几里得距离大于相应的MOD,
定理1:给定一个查询范围R和当前RONN结果集RS,一个R-树的条目e被过滤当且仅当对于R的每一个边$\bar{ab}$,满足$min_dist(e,\bar{ab})>max_odis(RS,\bar{ab})$,其中前者是欧几里得距离。
相比于CONNB算法,RONN-RF算法有两个优点:
- RONN-RF寻找外部RONN时,只需要遍历R-树一次,而CONNB需要四次
- RONN-RF通过启发式的方式来对搜索空间进行剪枝
以下是RONN-RF的算法流程:

七、O-树
R-树在处理RONN查询时,由于存在障碍,它面临两个问题。一个是需要在RONN-RF和CONNB中对R树进行多次遍历。在执行内部RONN(范围查询)和外部RONN查询时,RONN-RF需要遍历R树两次,而CONNB需要对R树进行五次扫描。另一个问题是在线计算有障碍距离是非常耗时的。
文章的想法是沿着选定的障碍物线和一些垂直线(如其平分线)将空间划分为四个子空间。我们递归地将子空间划分成更多的子空间来建立索引结构。
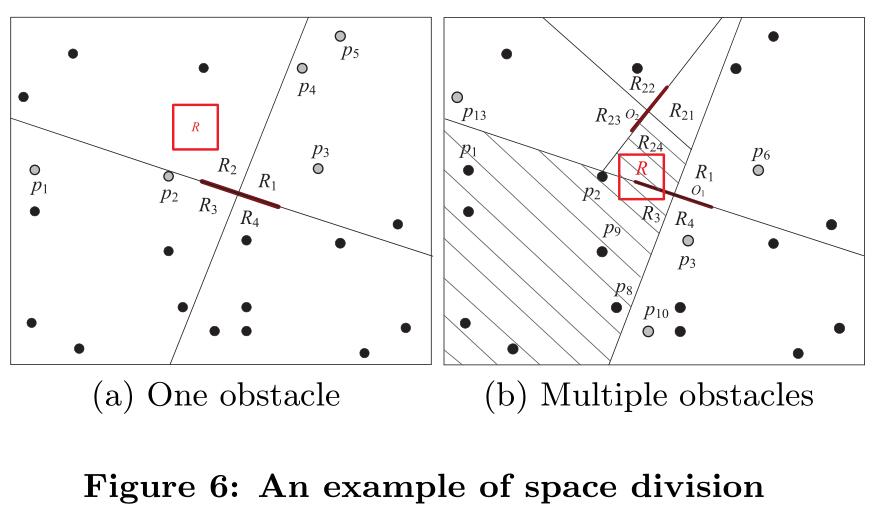
首先考虑一个只有一个障碍的有障碍子空间。图6(a)示出了这种有障碍空间的示例。通过沿障碍物及其垂直平分线划分空间,我们得到了四个无障碍子空间。
图6(a)中,不仅需要访问$R_2$中的黑圈,而且还需要访问$R_1、R_3$和$R_4$中的所有其他灰色圈来找到RONN,这显然会挫败我们O-树的最终目标。O-tree只需要存储由$R_2$中的黑色圆圈和灰色圆圈$p_1、p_2、…、p_5$表示的数据对象。如图6(b)所示,在查询处理中只需要检查$R_{24}$和$R_3$相关联的数据对象
会出现两个关键问题:首先应选择哪一个障碍来划分空间?对于给定的障碍物,其垂直平分线是划分空间的最佳选择吗?我们认为平衡的O-树是可取的,因此提出了实现树平衡的空间划分策略。在O-树中,由于障碍物被用来确定空间划分的支点,我们的目标是保持障碍物平衡,其定义如下:
定义7。障碍物平衡(obstacle balance):选择一个障碍物(障碍线及其垂直线)将空间划分为四个子空间。在每个划分步骤中,障碍物平衡由条件$|n_i−n_{i+1}|\leq1$($n_i$表示每个子空间中障碍物的数目)来满足,即每个分支的高度差小于1。
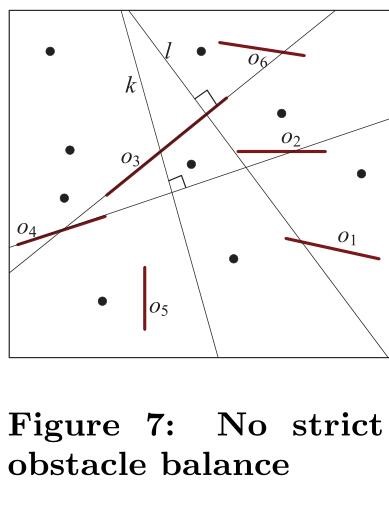
事实上,基于障碍物及其垂直线的选择,我们并不总是能够构造出一棵平衡树。从图7可以看出,如果我们选择$o_4$(或$o_3$)来划分空间,没有合适的垂直线来满足严格的障碍物平衡。在选择其他障碍物进行空间划分时,仍然存在同样的情况。
由于我们不能总是建立一个严格平衡树,我们的目标是建立一个最优的近似平衡树。因此,为了构造最优平衡树,我们提出了一种新的空间划分方案,称为最优障碍平衡(OOB)方案。
择一个障碍物(即障碍线)及其垂直线之一,将空间划分为四个子空间。目标是最小化目标函数$\Sigma(|n_i-n_j|)^2,i<j,i,j=1,2,3,4$,其中$n_i,n_j$表示进入两个不同子空间的障碍物的数量。
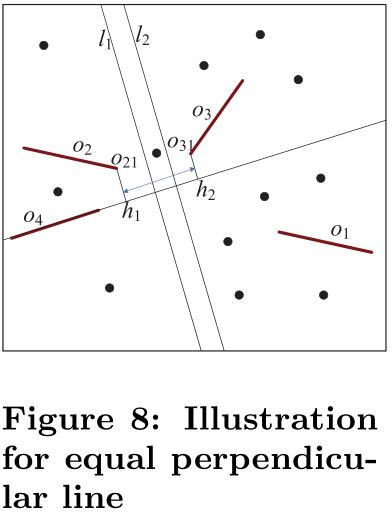
选择障碍物和垂直线的OOB方案:有n个障碍物,选择每个障碍物的花费是O(n),选定障碍物后再确定垂直线,这里以其他障碍物的端点在选定障碍线上的投影点做垂线从而得到垂直线,共有2(n-1)中可能,所以总时间复杂度为O(n*2(n-1))。如图8所示,选择$l_1$和$h_1、l_2$和$h_2$的效果是等价的,即一定范围的垂直线总是等于通过端点投影的一条垂直线。
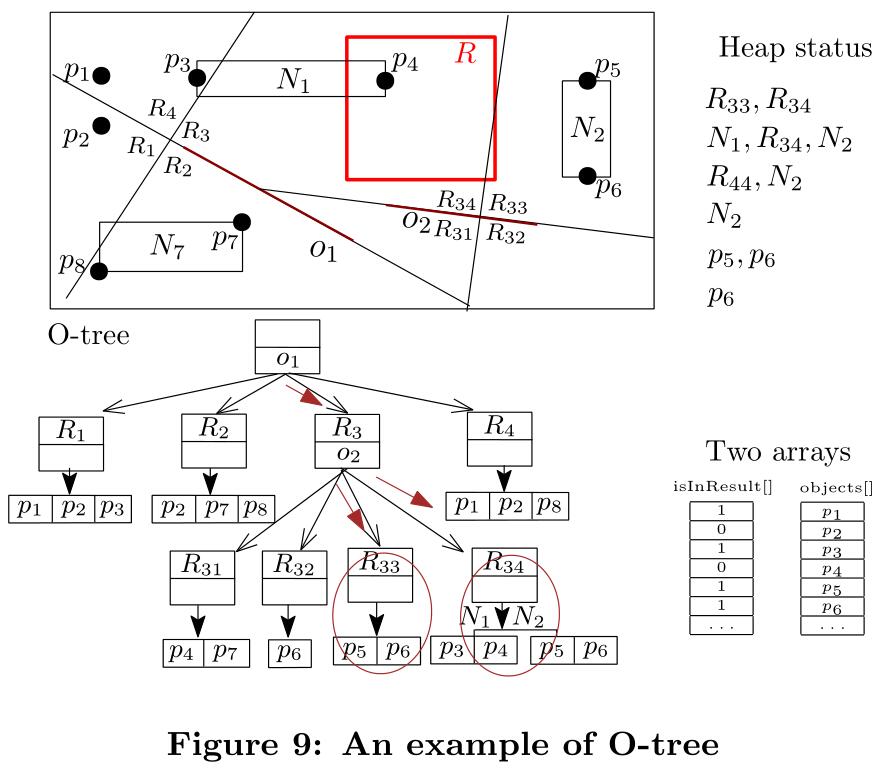
O树索引的结构如下。根节点表示整个有障碍空间,指向四个子节点。这些子节点中的每一个子节点表示有障碍空间中的一个区域。O-树的内部节点维护($reg$,$obs$,$optr_1$,$optr_2$,$optr_3$,$optr_4$)的条目,而叶节点包含形式(reg,rptr)的条目,其中reg表示二维多边形区域,obs是划分空间的障碍,optr i和rptr分别表示指向O-树和R-树节点的指针。图9示出了空间划分和对应的O树,图中实箭头是rptr,线箭头是optr。
由于O-tree索引存在一定的数据冗余,因此有两个潜在的问题:(i)索引大小增加;(ii)查询处理中同一数据对象可能存在冗余遍历。
为了减小索引的大小,我们将所有数据对象存储在一个 objects 数组中,并将每个对象的数组索引 id 存储在O树索引中。当测试数据对象 p 的时候,先查看其副本 p’ 是否在结果集中。还构建了一个与图9中的 objects 数组相关的 isInResult 数组。isInResult 数组标记数据对象是否在结果集中。

在构造了O树之后,通过调用CLN算法,用相应的R树填充O树索引的叶节点

先将叶节点内所有点插入到R树中,然后计算节点区域的每个边的ONNs,并将它们插入R-树。
八、RONN-OA
与RONN-RF类似,RONN-OA保持四个最大有障碍距离(MOD),以过滤不合格对象。RONN-OA首先发出一个范围查询以获取内部RONN,用于初始化四个MOD。值得注意的是,范围查询还返回与查询范围相交的O-tree的叶节点。接下来,在获得O-树的叶节点后,RONN-OA继续遍历相应的R-树来访问数据对象以找到外部RONN。在遍历R树期间,堆H用于存储R树条目。最初,H只包含与检索到的O树叶节点相关联的R树的根条目。RONN-OA的建堆和处理的过程与RONN-RF算法一致。
定理2:RONN-OA算法精确地检索给定查询范围内每个点的ONN,即该算法没有错误的未命中和错误的命中
九、实验
文章在3个真实的数据集上做了实验:
- Greece:将河流看作线段障碍,将城市和村庄看作数据对象;
- Tiger Census Blocks:包括美国多个州的人口普查块(看作多边形障碍);
- California Roads:把街道看作障碍,随机生成数据对象;
文章从两个方面进行性能评估:
- 评估RONN算法的效率:在各种参数下比较所提出的RONN算法的延迟(总结在表7中,粗体数字是默认设置);
- 评估O树的效率:我们比较高度、叶节点数,比较O-树的索引大小和构造时间对空间划分策略的影响。
索引了三种不同类型的障碍:
- 线段障碍(即数据集中的多段线);
- 矩形障碍(即数据集中的mbr);
- 多边形障碍。
使用SpatialDataGenerator随机生成五组具有不同查询大小的RONN查询,其中每组查询由50个RONN查询组成。文章使用了关于障碍物数、数据对象数量、查询大小相关的平均延迟作为度量标准。
障碍物数量的影响:通过增加障碍物的数量来比较三种处理RONN查询的算法的平均运行时间。查找内部RONN所需的时间非常短。正如预期的那样,当障碍物数量增加时,性能会变差,这三种算法在以矩形表示障碍物时都花费了更长的时间。这是因为需要在相应的可见性图中插入更多的障碍顶点;
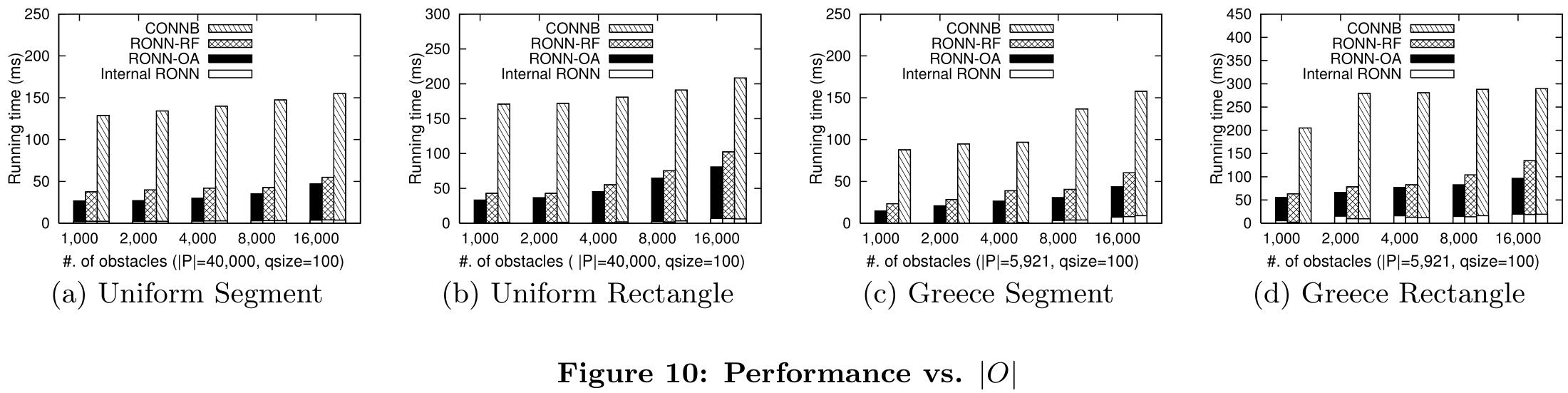
数据对象数量的影响:通过改变数据对象的数量来比较RONN算法的性能。而且,这三种算法的处理时间都随着数据对象数量的增加而增加;
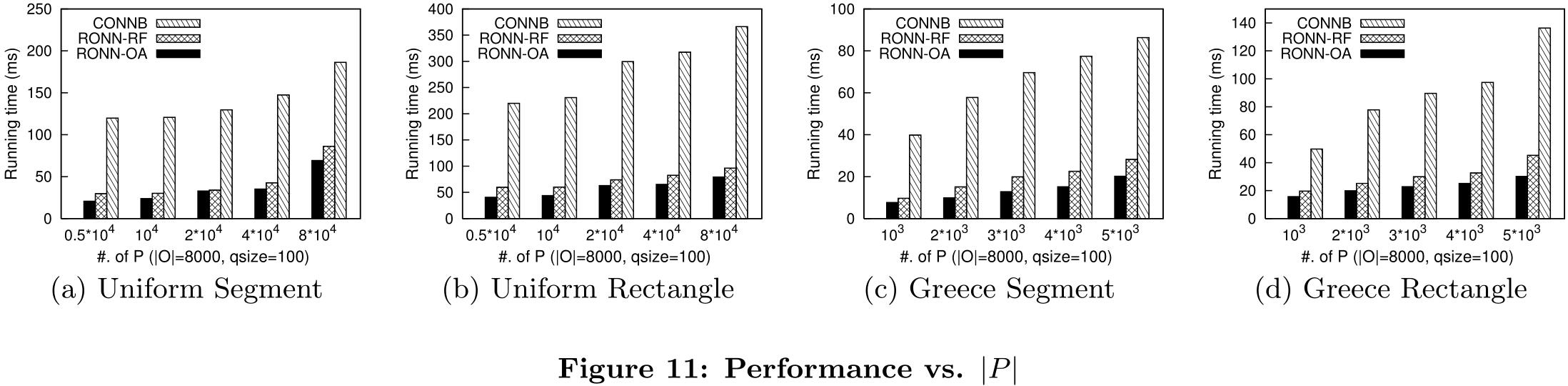
查询大小的影响:通过改变查询大小来比较RONN算法;
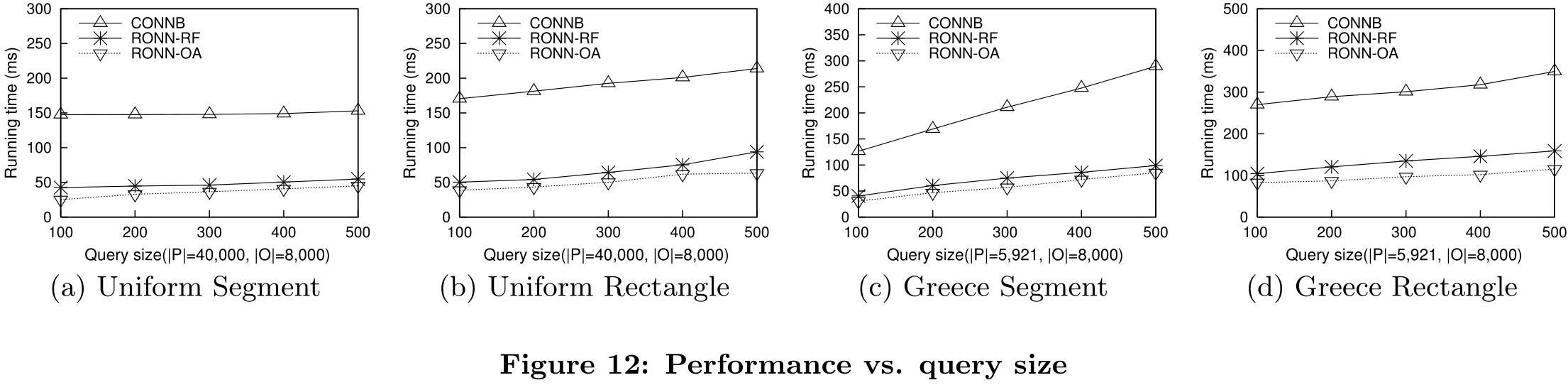
RONN-OA优于RONN-RF,因为O-tree索引可以过滤一些到查询范围的欧氏距离较小但到查询范围的阻塞距离较大的数据对象,而R-tree则不能过滤此类数据对象。
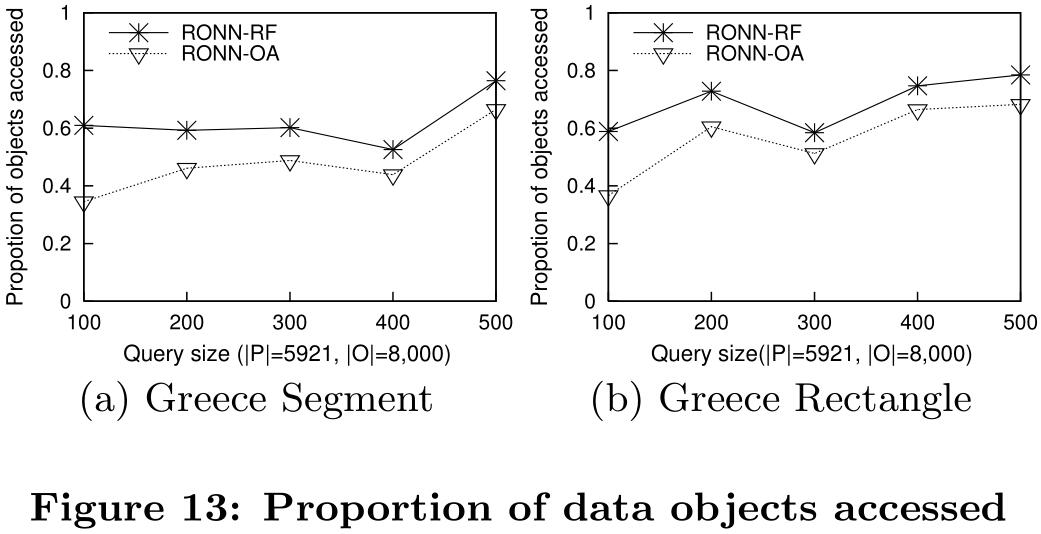
评估OOB方案的性能,并与以下两个基线方案进行比较:
- 随机:该方案在构造O-树时随机选择一个障碍物进行空间划分。
- Obs-Ctr:利用选定障碍物的垂直平分线作为空间划分的垂直线。它选择得分最高的障碍物来划分当前空间。
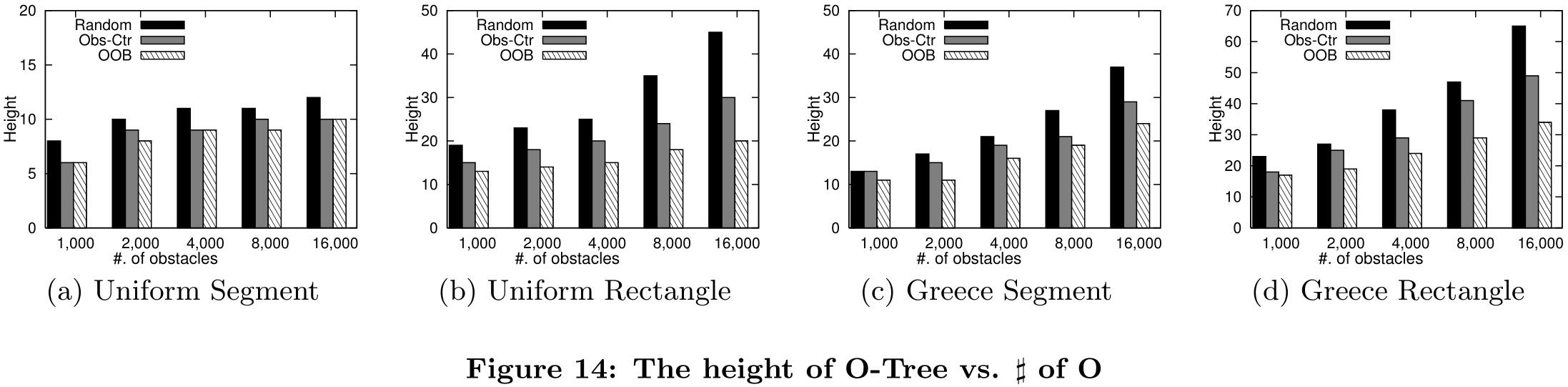
为了比较这些空间划分方案,使用对应的O-树的高度和叶节点作为性能指标,因为它们反映了这些O-树的平衡程度,即叶节点的高度和数量越小,树的平衡越好。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/05/25/RONN/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


