本文是论文《Linear and Deformable Image Registration with 3D Convolutional Neural Networks》的阅读笔记。
一、概述
文章提出了一个可以实现线性和可变形(deformable)配准的模型。
可变形配准的目标是计算一个最优的非线性密度变换$G$来将源(浮动)图像$S$对齐到参考(目标)图像$R$,得到配准后的源图像$D$。基于深度学习的配准通常有以下缺陷:
- 依赖于变换的线性分量;
- 依赖于用作监督学习的ground truth位移场。
文章的主要贡献如下:
- 在同一个网络结构中同时解决了线性和可变形配准问题;
- 一个不依赖不同相似性度量的模块化、无参数的实现;
- 减少了配准的时间,实现了配准的实时性;
- 将变形(deformation)和临床信息联系起来。
二、方法
在下文中,变形(deformation)、网格(grid)和转换(transformation)将是同一个意思,即可互换的。
1. 线性和可变形转换
3D转换层(类似于空间转换网络,STN)是配准网络的一个重要组成部分,它可以根据变形$G$将输入图像$S$进行变换得到图像$D$,即:
$$
D=\mathcal{W}(S, G)
$$
其中$\mathcal{W}(\cdot,G)$表示在变形$G$下的采样操作$\mathcal{W}$,$G$是密度变换。
采样过程可以用下式来表示:
$$
D(\mathbf{p})=\mathcal{W}(S, G)(\mathbf{p})=\sum_{\mathbf{q}} S(\mathbf{q}) \prod_{d} \max \left(0,1-\left|[G(\mathbf{p})]{d}-\mathbf{q}{d}\right|\right)
$$
其中,$p,q$表示体素位置,$d\in{x,y,z}$表示一个轴,$|G(p)|_d$表示$G(p)$的第$d$个分量。
线性(仿射)配准需要根据$[\hat{x}, \hat{y}, \hat{z}]^{T}=A[x, y, z, 1]^{T}$预测一个$3\times4$的仿射变换矩阵$A$,其中$[x, y, z, 1]^{T}$表示需要变形的增广点,$[\hat{x}, \hat{y}, \hat{z}]^{T}$表示在变形后的图像中它们的位置。然后就可以用矩阵$A$得到一个采样网格$G_A$来进行采样。
可变形配准部分$G_N$是直接生成一个用来采样每个体素的采样坐标。如果没有合适的正则项,那么将会产生不平滑甚至不相关的变形,为了避免这个问题,采取的办法是在每个维度预测变形的空间梯度$\phi$,而不是直接预测变形本身。接下来在每个维度进行集成操作,即通过在每个维度进行简单的累加来实现。例如,当$\Phi_{\mathbf{p}{d}}=1$时,在变形后的图像的$d$轴上的体素$p$和$p+1$之间的距离没有变化;当$\Phi{\mathbf{p}{d}}<1$时,$d$轴上连续体素之间的距离将会减少;反之,当$\Phi{\mathbf{p}_{d}}>1$时,距离将会增加。这种方式可以产生平滑的形变场以避免自交叉。
为了组合这两个部分,先对运动图像应用可变形分量,然后再应用线性分量,即:
$$
\mathcal{W}(S, G)=\mathcal{W}\left(\mathcal{W}\left(S, G_{N}\right), G_{A}\right)
$$
2. 网络结构
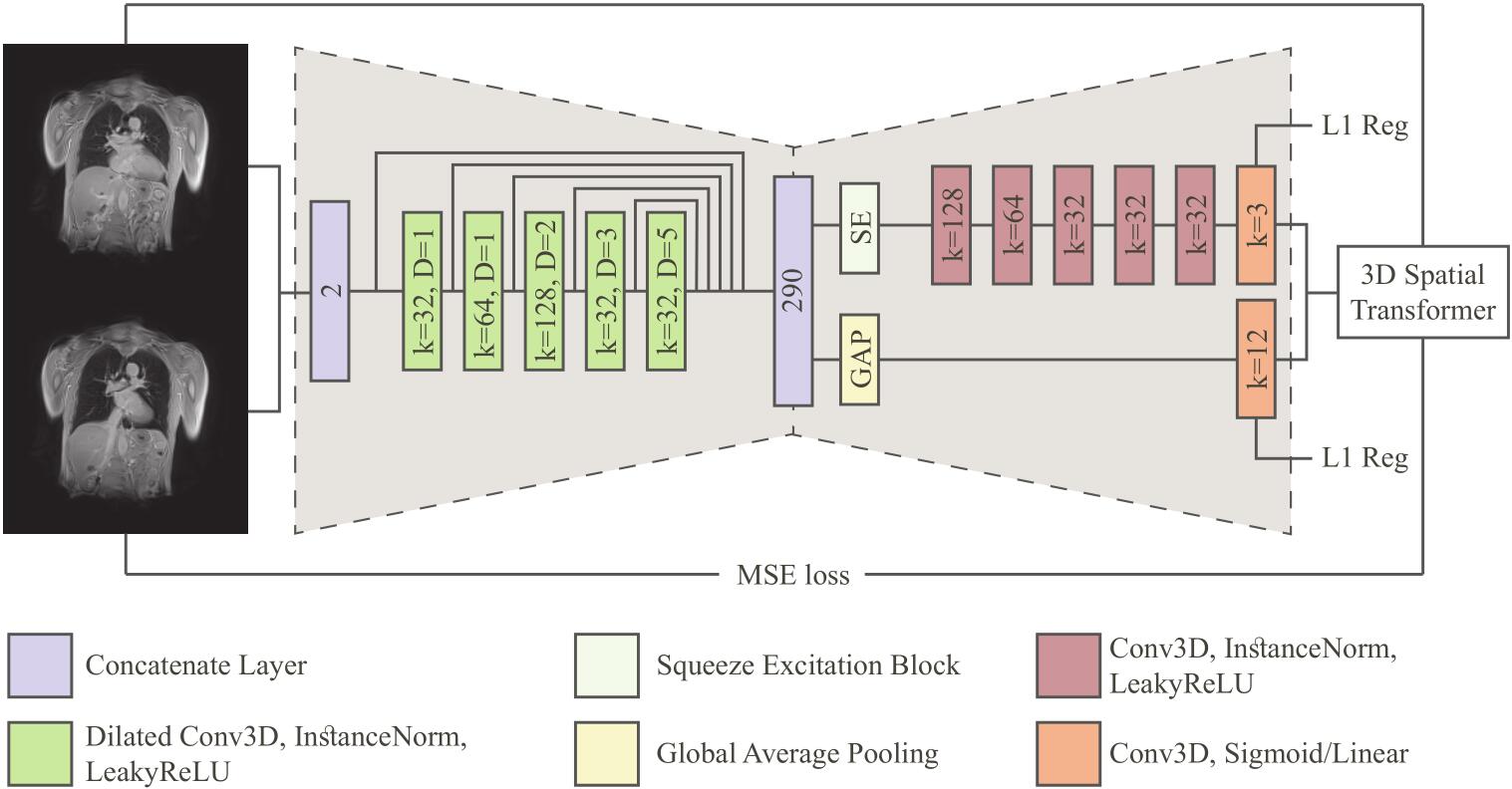
模型的网络结构如上图所示,网络包括编码器和解码器两部分,编码器采用的是空洞卷积,并且进行了多分辨率特征合并;解码器部分采用的是普通卷积和上采样操作。卷积核的大小是$3\times3\times3$,除了最后两层都以Leaky ReLU作为激活函数,在多数激活函数前使用了实例正则化操作。在编码器中一共有5层,每层的输出经过合并后得到编码器的输出,形成接收域为$25\times25\times25$,有290个特征的特征图。解码器有两个分支,一个是就散空间变形的梯度,另一个是计算仿射矩阵。第一个分支加入了squeeze-excitation块,用来加权空间梯度计算中最重要的特征;第二个分支使用了一个全局平均操作来减少空间维度到一维。这两个分支分别采用了sigmoid和线性激活函数。sigmoid激活函数后还需要乘以2,以让输出范围在[0,2]之间。
3. 训练
模型采用的MSE来评价图像的相似性,使用Adam作为优化器,模型的损失为:
$$
\operatorname{Loss}=|R-\mathcal{W}(S, G)|^{2}+\alpha\left|A-A_{I}\right|{1}+\beta\left|\Phi-\Phi{I}\right|_{1}
$$
其中$A_I$表示恒等仿射变换矩阵,$\phi_I$表示恒等变换的空间梯度,$\alpha,\beta$是正则化权重。如果没有$A$上的$L1$正则化,则网络可能陷入局部最小值,此时只能使用仿射变换对齐高维特征;如果没有$\phi$上的平滑正则项,空间梯度编码器网络会生产不平滑的网格,从而陷入局部最小值。
初始学习率为$10^{-3}$,如果在验证集上50个epoch效果没有提升,则学习率变为之前的十分之一,当100个epoch效果没有提升时,则停止训练,一共训练300个epoch。$\alpha=\beta=10^{-6}$,batch size为2,没100个batch就会评估一次训练的效果。
三、实验
选用的baseline是ANTs包中的SyN,相似性度量有衡量配准后肺部mask标签的NCC、MI、DWM(discrete wavelet metric)。此外还会使用提供的地标位置来计算配准后的误差。
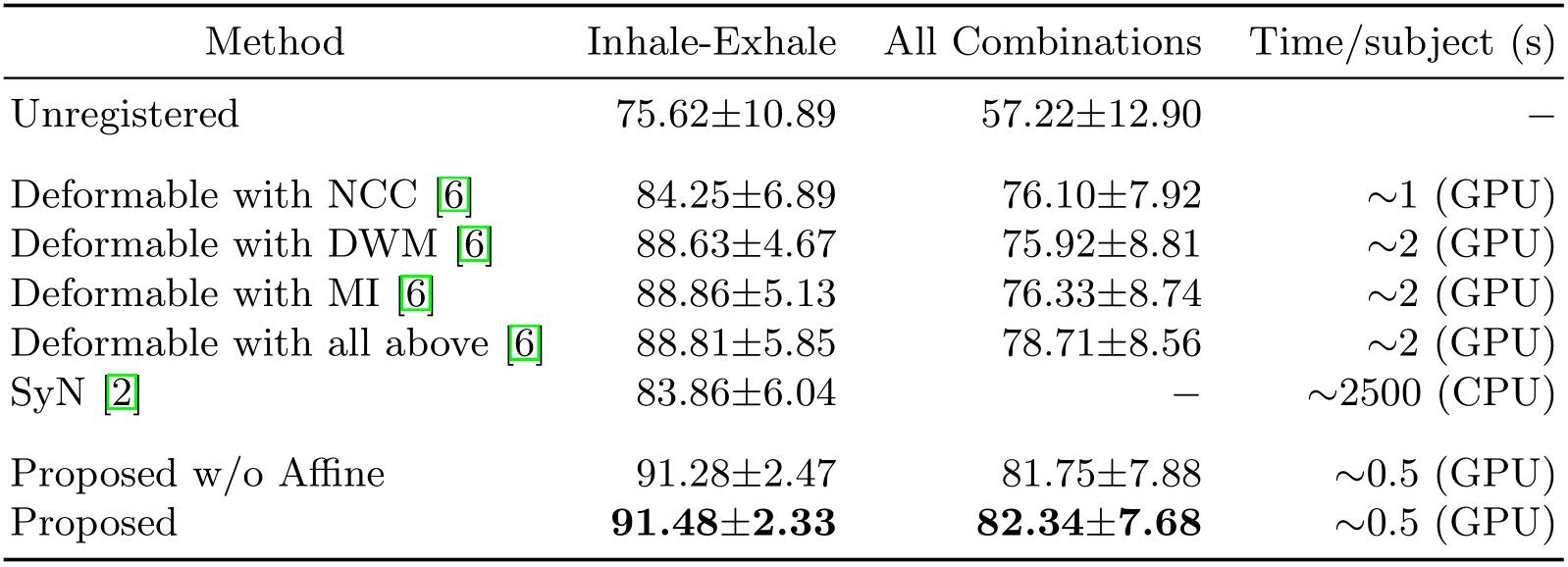
在第一组实验中,用不同的方法对吸气和呼气时的肺部MRI图像进行配准,并对比其效果,如上表所示;测试了三种不同的相似性度量标准,以及它们组合使用的效果,MI度量产生了最高的Dice值;实验表示,对于本文提出的模型来说,在转换层添加一个线性分量不会明显的改变模型的性能;最后计算了配准后11个地标点在每个轴的误差。

上表展示了不同方法在变形后图像的地标点和ground truth图像的地标点之间的欧几里得距离,其中Inter-observer是两个专家在同一个图片上标记地标点之间的欧几里得距离。$d_x,d_y,d_z$分别是在$x,y,z$轴上的距离,$d_s$是所有轴上的平均误差。
第二组实验,使用13个病人的组合来得到Dice值,发现线性分量的作用更重要。
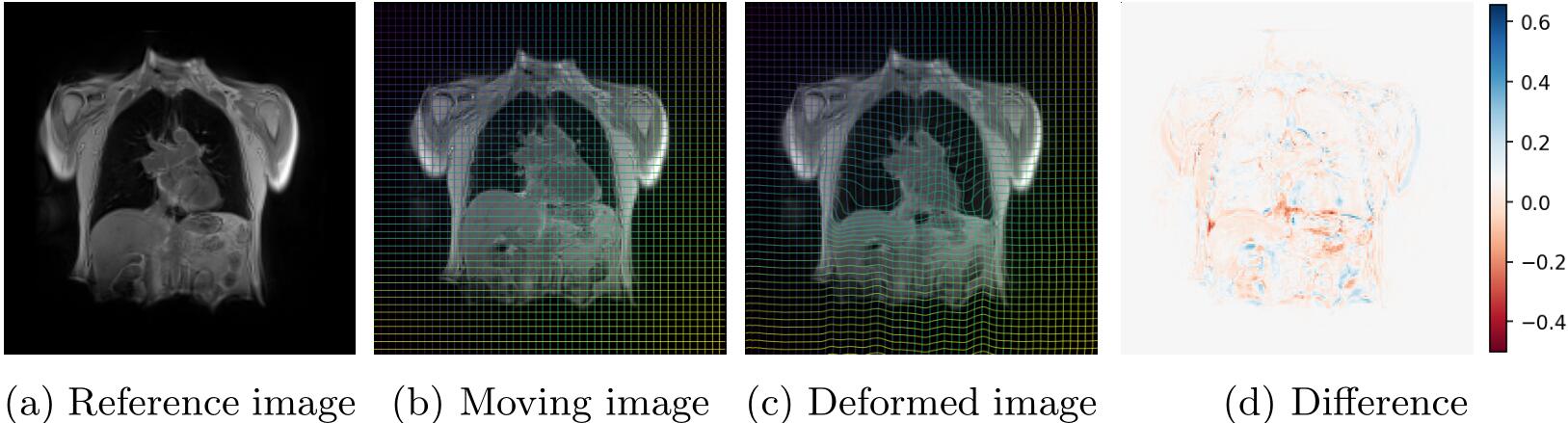
上图展示了模型的配准效果。
为了评估解码后的转换在临床环境中的相关性,我们在获得的残余变形(residual deformation)上训练了一个小分类器来将患者分为健康或不健康。残余变形和一对表示体素位移的图像相关,写为:$G_\sigma=G-G_I$,其中$G$是两张图像推测的变形,$G_I$是恒等变形。具体的使用了一个MLP(多层感知机)来预测一个样例是健康还是不健康。该模型包括批量正则化以避免过拟合,激活函数使用的是Tanh,下采样的卷积核大小为$3\times3\times3$,步长为2,填充为1。隐藏层的单元数为100。使用二值交叉熵损失,学习率为$10^{-4}$,每经过50个epoch学习率减半。在测试集上的阈值为0.5。
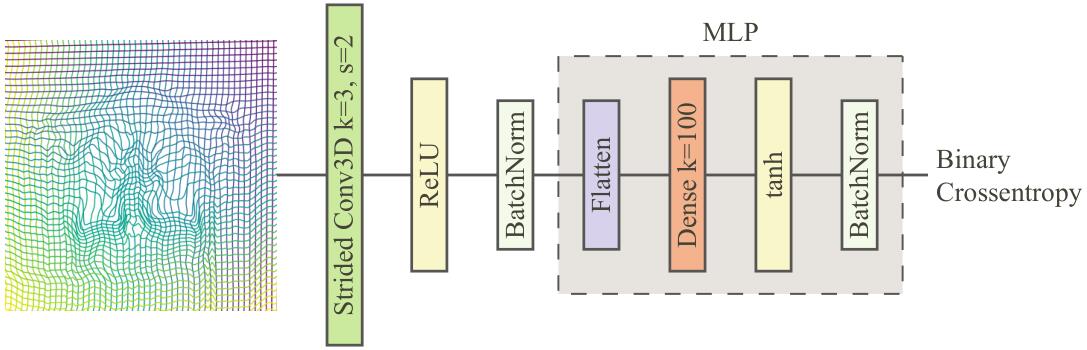
上图是上述MLP的结构示意图。

上表是在测试集上疾病预测的准确率。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/08/09/LDIR/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


