本文是论文《Unsupervised Learning for Fast Probabilistic Diffeomorphic Registration》的阅读笔记。涉及数学的东西太多,没搞懂是怎么做的。
一、微分同胚
现有的基于学习的配准方法通常不能保证配准是微分同胚的,即保留拓扑性的(topology-preserving)。
本文在VoxelMorph模型的基础上加入了微分同胚积分层(diffeomorphic integration layer),以保证无监督的端到端的学习是微分同胚的。微分同胚是可微和可逆的,因此保留了拓扑性。形变场是通过下述常微分方程(OED)来定义的:
$$
\frac{\partial \phi^{(t)}}{\partial t}=\boldsymbol{v}\left(\phi^{(t)}\right)
$$
其中,$\phi^{(0)}=Id$是恒等变换,$t$是时间,用静态速度场(stationary velocity field)$v$对$t=[0,1]$积分得到最终的配准场$\phi^{(1)}$。使用缩放和展平(squaring)来计算积分,静态ODE的积分可以表示为微分同胚的单参数子群,在群论中,$v$是李代数的一员,并且求幂得到$\phi^{(1)}$,$\phi^{(1)}$是李群$\phi^{(1)}=\exp(v)$的一员。从单参数子群的属性可知,对于任意常量$t$和$t’$,有$\exp((t+t’)v)=\exp(tv)\circ\exp(t’v)$,其中$\circ$是和李群相关的成分图(composition map)。从$\phi^{\left(1 / 2^{T}\right)}=\boldsymbol{p}+\boldsymbol{v}(\boldsymbol{p}) / 2^{T}$开始,使用重现(recurrence)$\phi^{\left(1 / 2^{t-1}\right)}=\phi^{\left(1 / 2^{t}\right)} \circ \phi^{\left(1 / 2^{t}\right)}$来获取$\phi^{(1)}=\phi^{(1 / 2)} \circ \phi^{(1 / 2)}$,其中$p$是空间位置的映射,选择$T$使得$v/2^T\approx 0$。
二、Prob-VoxelMorph
让$x,y$表示3维MR图像,$z$表示转换函数$\phi_z$的隐变量,将$z$的先验概率表示为:
$$
p(\boldsymbol{z})=\mathcal{N}\left(\boldsymbol{z} ; \mathbf{0}, \boldsymbol{\Sigma}{z}\right)
$$
其中$\mathcal{N}\left(\boldsymbol{z} ; \mathbf{0}, \boldsymbol{\Sigma}{z}\right)$是多远正态分布,$\mu$和$\Sigma$分别是其均值和方差。$z$可以是形变场的低维嵌入,也可以是形变场本身。在本文中,让$z$表示静态形变场。让$L=D-A$表示定义在体素网格上的邻接图的拉普拉斯,其中$D$是图的度矩阵,$A$是体素邻接矩阵。通过让$\boldsymbol{\Sigma}{z}^{-1}=\boldsymbol{\Lambda}{z}=\lambda \boldsymbol{L}$来保证$z$的空间平滑,其中$\boldsymbol{\Lambda}{z}$是精密矩阵(precision matrix)。我们让$x$是扭曲图像$y$的噪声观测:
$$
p(\boldsymbol{x} \mid \boldsymbol{z} ; \boldsymbol{y})=\mathcal{N}\left(\boldsymbol{x} ; \boldsymbol{y} \circ \boldsymbol{\phi}{z}, \sigma^{2} \mathbb{I}\right)
$$
其中$\sigma^2$是加性图像的方差。
我们的目标是估计后验配准概率$p(z|x;y)$,使用变分的方法,引入一个近似后验概率$q_{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})$,通过最小化以下KL散度(即变分下界的负)来计算:
$$
\begin{array}{l}
\min {\psi} \mathrm{KL}\left[q{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y}) | p(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})\right] \
=\min {\psi} \mathbf{E}{q}\left[\log q_{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})-\log p(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})\right] \
=\min {\psi} \mathbf{E}{q}\left[\log q_{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})-\log p(\boldsymbol{z}, \boldsymbol{x}, \boldsymbol{y})\right]+\log p(\boldsymbol{x} ; \boldsymbol{y}) \
=\min {\psi} \mathrm{KL}\left[q{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y}) | p(\boldsymbol{z})\right]-\mathbf{E}{q}[\log p(\boldsymbol{x} \mid \boldsymbol{z} ; \boldsymbol{y})]
\end{array}
$$
近似后验概率$q{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})$可以表示为:
$$
q_{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})=\mathcal{N}\left(\boldsymbol{z} ; \boldsymbol{\mu}{z \mid x, y}, \boldsymbol{\Sigma}{z \mid x, y}\right)
$$
其中$\Sigma_{z|x;y}$是对角矩阵。
使用参数为$\psi$的卷积神经网络$def_\psi(x,y)$来估计$\mu_{z|x,y}$和$\Sigma_{z|x,y}$,可以通过随机梯度下降的方法优化变分下界来学习参数$\psi$,给定图像对${x,y}$和样例$\boldsymbol{z}{k} \sim q{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})$,通过以下损失来计算$y\circ\phi_{zk}$:
$$
\begin{array}{l}
\mathcal{L}(\psi ; \boldsymbol{x}, \boldsymbol{y})=-\mathbf{E}{q}[\log p(\boldsymbol{x} \mid \boldsymbol{z} ; \boldsymbol{y})]+\mathrm{KL}\left[q{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y}) | p(\boldsymbol{z})\right] \
=\frac{1}{2 \sigma^{2} K} \sum_{k}\left|\boldsymbol{x}-\boldsymbol{y} \circ \boldsymbol{\phi}{z{k}}\right|^{2}+\frac{1}{2}\left[\operatorname{tr}\left(\lambda \boldsymbol{D} \boldsymbol{\Sigma}{z \mid x ; y}-\log \left|\boldsymbol{\Sigma}{z \mid x ; y}\right|\right)+\boldsymbol{\mu}{z \mid x, y}^{T} \boldsymbol{\Lambda}{z} \boldsymbol{\mu}{z \mid x, y}\right]+\mathrm{const}
\end{array}
$$
其中$K$是样例的个数,在实验中使用$K=1$。上式中第一项可以让配准后的图像$y\circ\phi{zk}$和$x$相似,第二项鼓励后现概率接近于先验概率$p(z)$。虽然变分协方差$\Sigma_{z|x,y}$是对角矩阵,但是最后一项在空间上平滑了均值:$\boldsymbol{\mu}{z \mid x, y}^{T} \boldsymbol{\Lambda}{z} \boldsymbol{\mu}{z \mid x, y}=\frac{\lambda}{2} \sum \sum{j \in N(I)}(\boldsymbol{\mu}[i]-\boldsymbol{\mu}[j])^{2}$,其中$N(i)$是体素$i$的邻居,将$\sigma^2$和$\lambda$看作是固定的超参数。
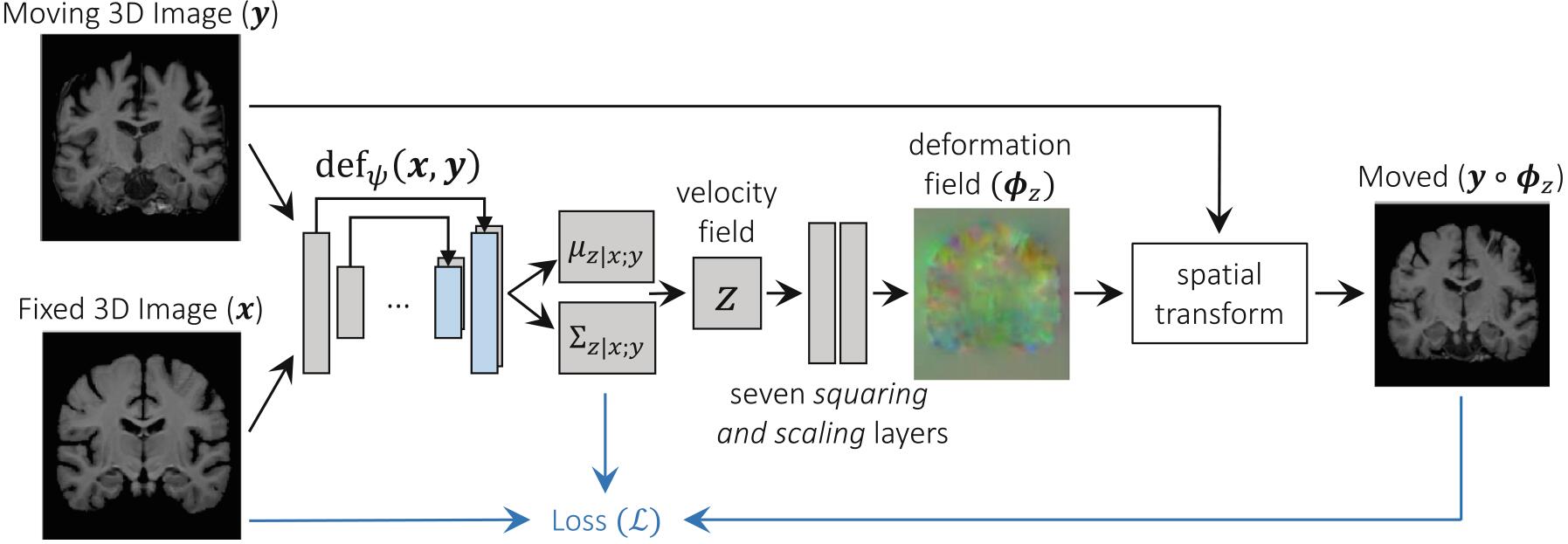
卷积神经网络$def_\psi(x,y)$的输入是图像$x,y$,输出是$\mu_{z|x,y}$和$\Sigma_{z|x,y}$。神经网络包括一个卷积层(16通道),4个下采样层(32通道,步长为2)和3个上采样卷积层(32通道),每个卷积层后跟着Leaky ReLU激活函数,并且卷积核大小为$3\times3$。模型的结构如上图所示。
为了使用公式(6)进行无监督的学习,使用了一个通过重参数化技巧来采样一个新的$\boldsymbol{z}{k} \sim \mathcal{N}\left(\boldsymbol{\mu}{z \mid x, y}, \boldsymbol{\Sigma}_{z \mid x, y}\right)$。
文章提出了缩放和展平层来计算$\phi_{z_k}=\exp(z_k)$,给定两个3D向量场$a$和$b$,对于每个体素$p$,使用线性插值计算$(a\circ b)(p)=a(b(p))$,即$a$中一个非整数的体素位置$b(p)$。开始时有$\phi^{\left(1 / 2^{T}\right)}=\boldsymbol{p}+\boldsymbol{z}{k} / 2^{T}$,递归的计算$\boldsymbol{\phi}^{\left(1 / 2^{t+1}\right)}=\boldsymbol{\phi}^{\left(1 / 2^{t}\right)} \circ \boldsymbol{\phi}^{\left(1 / 2^{t}\right)}$,使得$\phi^{(1)} \triangleq \phi{z_{k}}=\exp \left(\boldsymbol{z}_{k}\right)$,在本文中$T=7$。
三、处理过程
总结一下就是,卷积神经网络$def_\psi(x,y)$以$x,y$为输入,计算$\mu_{z|x,y}$和$\Sigma_{z|x,y}$,采样一个新的$\boldsymbol{z}{k} \sim \mathcal{N}\left(\boldsymbol{\mu}{z \mid x, y}, \boldsymbol{\Sigma}{z \mid x, y}\right)$,计算微分同胚$\phi{z_k}$并将其作用在$y$上。
给定已经学习好的参数,使用$\phi_{\hat{z}{k}}$来对图像对$(x,y)$进行近似配准,首先使用以下公式获取$\hat{z_k}$:
$$
\hat{\boldsymbol{z}}{k}=\arg \max {z{k}} p\left(\boldsymbol{z}{k} \mid \boldsymbol{x} ; \boldsymbol{y}\right)=\boldsymbol{\mu}{z \mid x ; y}
$$
然后使用缩放和展平层计算$\phi_{\hat{z_k}}$,我们还得到$\Sigma_{z|x,y}$,可以估计每个体素$j$处速度场$z$的不确定性:
$$
H(\boldsymbol{z}[j]) \approx \mathbf{E}\left[-\log q_{\psi}(\boldsymbol{z} \mid \boldsymbol{x}, \boldsymbol{y})\right]=\frac{1}{2} \log 2 \pi \boldsymbol{\Sigma}{z \mid x ; y}[j, j]
$$
我们也估计形变场$\phi_z$的不确定性。采样几个表达$\boldsymbol{z}{k^{\prime}} \sim q_{\psi}(\boldsymbol{z} \mid \boldsymbol{x} ; \boldsymbol{y})$,通过微分同胚层传播它们来计算$\phi_{z’k}$和经验对角协方差(empirical diagonal covariance)$\hat{\Sigma}{\phi_z}[j,j]$,不确定性为$H(\phi[j])\approx\frac{1}{2}\log 2\pi\hat{\Sigma}_{\phi_z}[j,j]$。
四、实验
实验部分进行了基于3D atlas的配准,使用的数据集有ADNI,OASIS,ABIDE,ADHD200,MCIC,PPMI,HABS和Harvard GSP。首先对数据进行标准预处理:将图像重采样成1mm的各向同性体素,并用FreeSurfer进行反射空间正则化和脑部提取(头骨去除),然后将图像裁剪到$160\times192\times224$大小。按照7329,250,250大小分别划分为训练集、验证集和测试集。
将配准得到的形变场作用在分割标签上,并计算其Dice score。为了验证微分同胚性,使用了雅克比矩阵$J_\phi(p)=\nabla\phi(p)\in R^{3\times3}$,雅克比矩阵可以捕获形变场$\phi$在体素$p$处的局部特性。只有在满足$|J_\phi(p)|>0$的位置,局部形变才是微分同胚的,即可逆和方位保持(orientation-preserving)的。
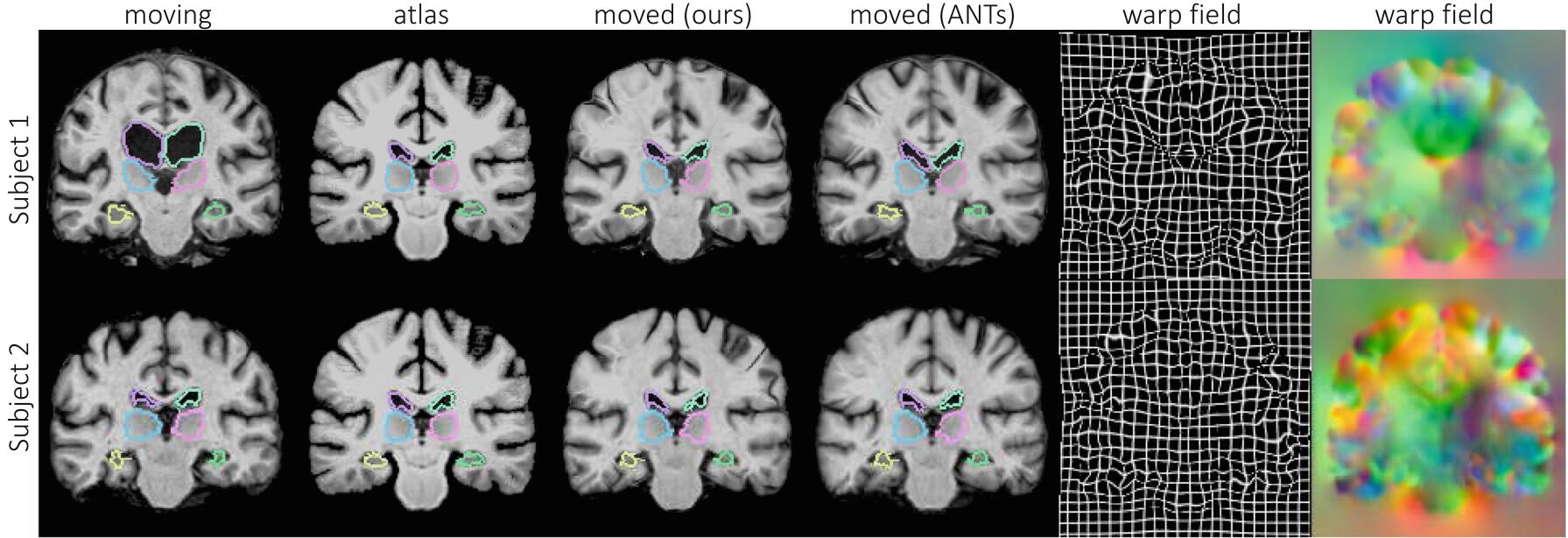
baseline选用的是ANTs软件包中的SyN和VoxelMorph,后者不能保证形变场是微分同胚的或者是不确定的估计。上图两行分别是本文的方法和ANTs的配准结果对比,VoxelMorph的和ANTs的类似,没有画出。
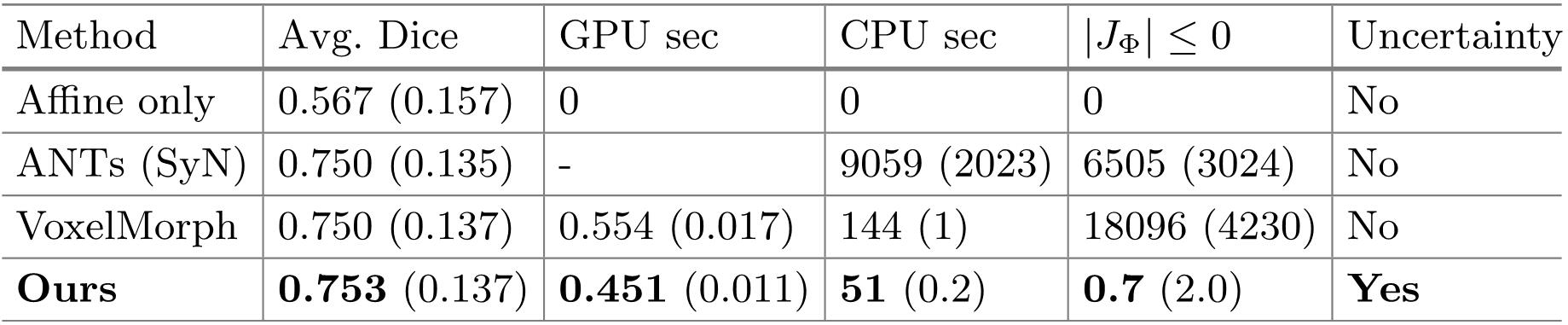
由上图可知,本文所提出的模型不仅在Dice值上达到了最好的水平,而且运行时间更快,并且配准形变场是微分同胚的(几乎没有非负的雅克比体素)。
通过是实验发现$\sigma^2\sim(0.035)^2$并且$\lambda\in(2w,10w)$时效果最好,本文中使用的是$\lambda=7w$。
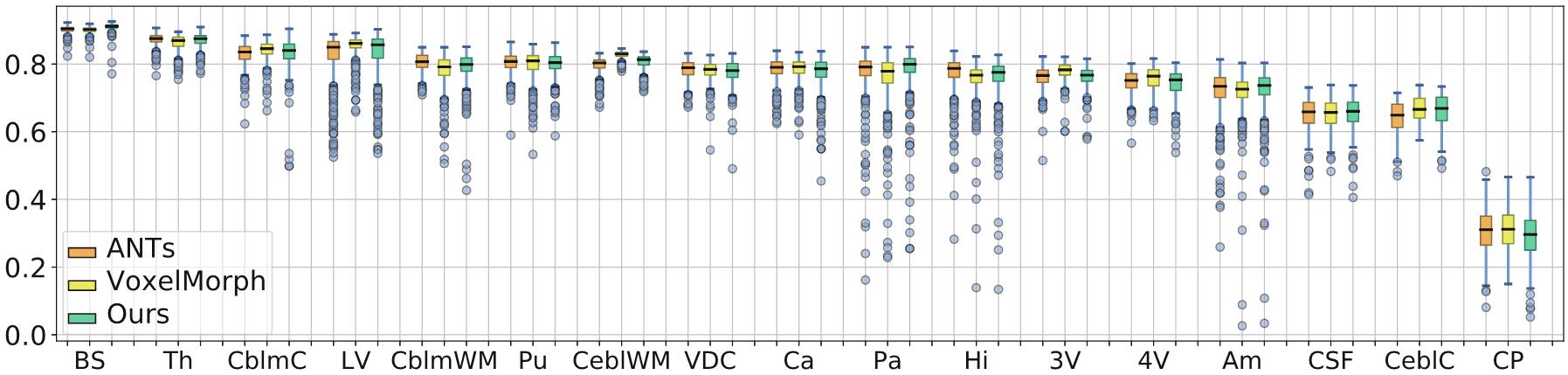
上图是ANTs、VoxelMorph和本文配准结果在脑部各个结构的Dice值对比。
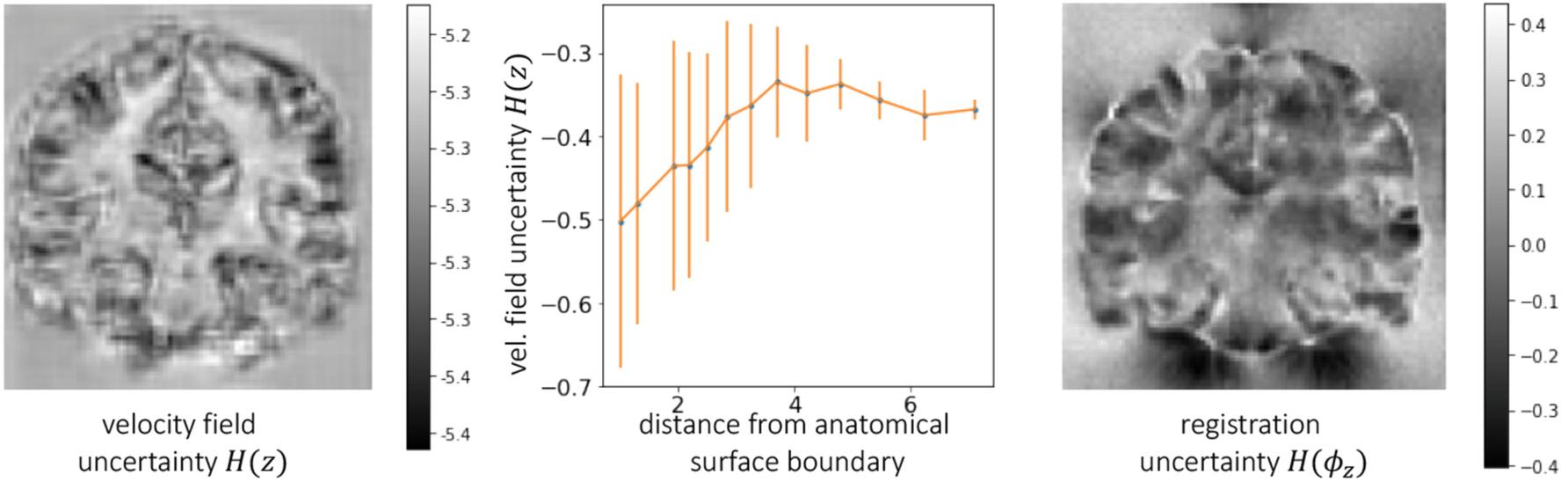
上图中的左图的速度场的不确定性$H(z)$表明了在结构边缘的低不确定性,如中间的折线图所示,这种相关性在最终的配准场的不确定性$H(\phi_z)$中并不明显,如右图所示。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/08/04/Prob-VoxelMorph/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


