本文是论文《FAIM – A ConvNet Method for Unsupervised 3D Medical Image Registration》的阅读笔记。
文章提出了一个用于3D医学图像的无监督配准模型FAIM(FAst IMage registration),相比于VoxelMorph,FAIM拥有更少的可学习参数,但是能达到更好的性能。此外FAIM提出了一个负的雅克比行列式的惩罚性损失(防重叠正则化项),以使得预测的形变场具有更少的重叠,重叠的部分表示形变是不可逆的。文章相应的代码见FAIM代码。
一、相关工作
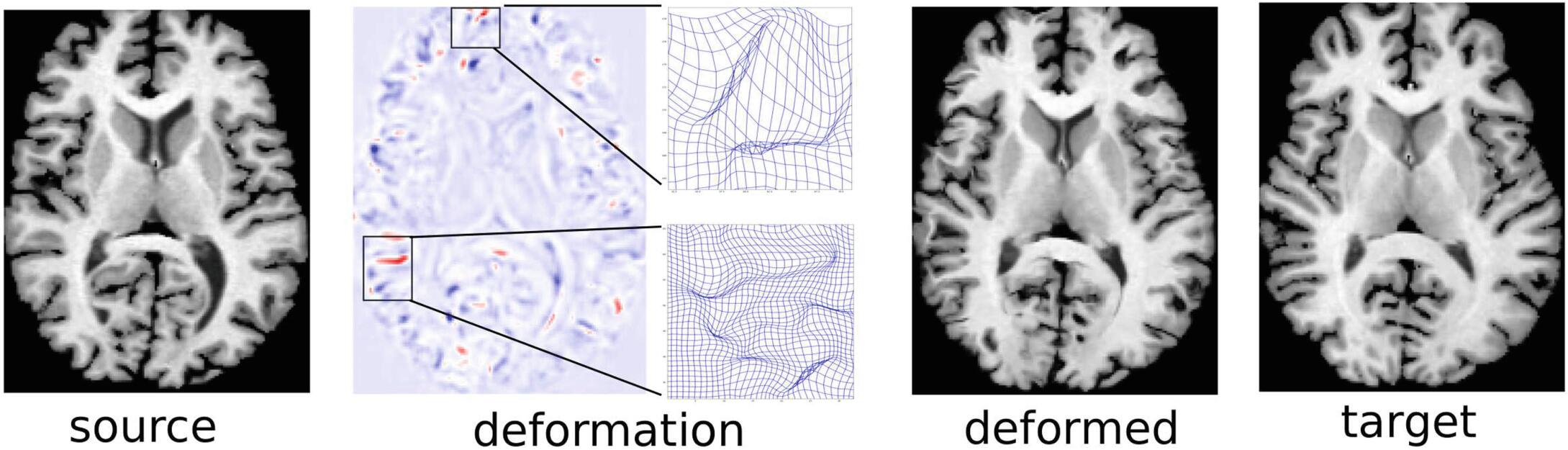
已有的基于学习的配准方法通常不能保证预测的形变场是微分同胚的,即可逆和可微的。由于形变场很多地方可能是重叠的,表明该转换是不可逆的。图是是通过VoxelMorph配准得到图像,deformation图中红色的部分表示形变场中重叠的部分,即雅克比行列式为负的地方。
空间转换网络(STN)一开始只是用于2D图像的仿射和薄板样条变换,后来才逐渐用于3D的图像变换。配准是为了优化一个参数化的转换$\phi$,使得从源图像$S(x)$转换得到的图像$S\circ\phi^{-1}(x)$与目标图像$T(x)$尽可能的相似。在FAIM中,使用位移场$u(x)$来参数化转换$\phi$,即$S\circ\phi^{-1}(x)=S(x+u(x))$。位移的3D向量场通过空间变换模型(spatial deformation module,SDM)得到。
二、FAIM
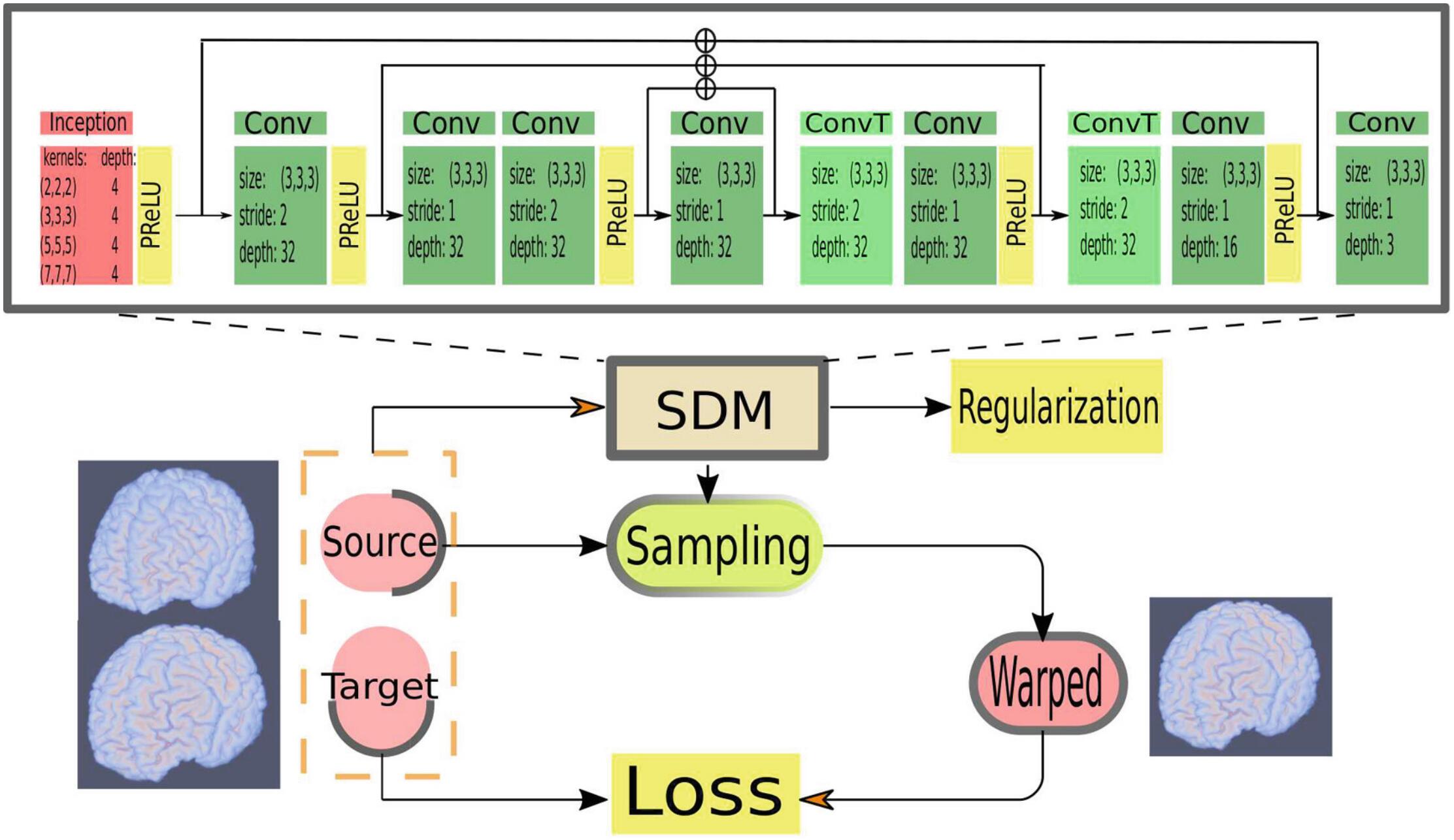
网络模型结构如上图所示,SDM的第一层收到了GoogLeNet的Inception模型的启发,该层可以对比和捕获不同空间尺度的信息。在每个卷积层的后面都跟着一个PReLU激活函数,最后一个卷积层除外,它后面跟着的是一个线性激活函数来产生位移场。采样模型首先根据位移场产生一个采样网格,然后用它来对源图像通过插值的方法进行采样,得到变形后的图像。在SDM中,使用步长>1的卷积来减小特征图的大小,而不是使用最大池化层。Transposed卷积层用作上采样。并且SDM中还有3个跳跃连接操作。相比于VoxelMorph中使用的Unet网络结构,FAIM中的SDM的参数减少了约30%。
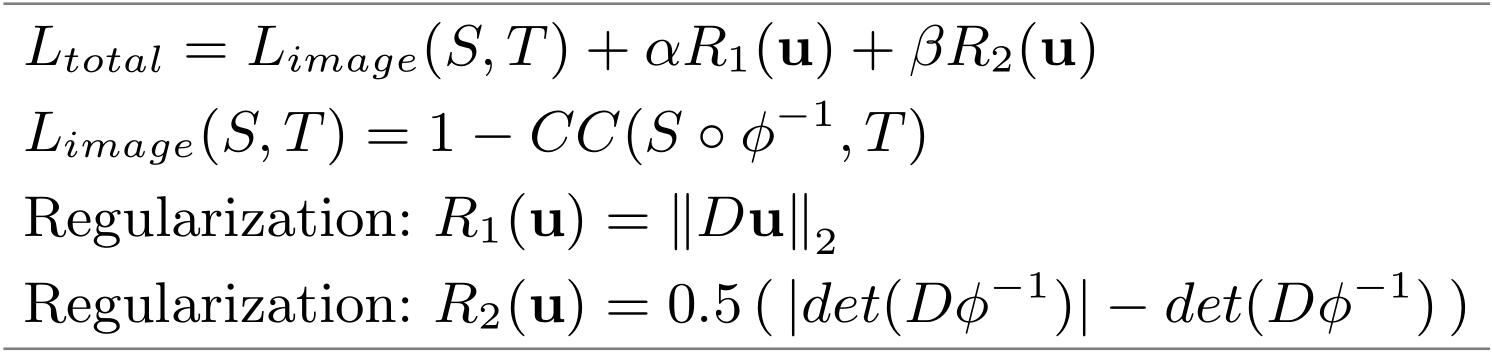
上图是训练损失,其中$L_{image}$是基于互相关(CC)的图像相似度损失,$R_1$是使得预测的位移场平滑的正则项,$R_2$是惩罚具有较多负的雅克比行列式的形变场的正则项。
三、实验
实验使用的是MindBoggle101数据集,该数据集包括三个子数据集:
- NKI-RS-22
- NKI-TRT-20
- OASIS-TRT-20
将NKI-RS-22和NKI-TRT-20作为训练集,将OASIS-TRT-20作为测试集。使用FreeSurfer对所有图像进行预处理,然后使用其DK皮层分组图谱自动标记皮层。每个图像都是$182\times218\times182$大小的,然后裁剪到$144\times180\times144$大小,这些图像已经对齐到MNI152空间,还需要将其灰度值归一化到[0, 1]的范围。
实验具体设置为$\alpha=1$,epoch=10,选用学习率为$1e^{-4}$的Adam优化器,使用VoxelMorph作为baseline,使用Dice值作为评价指标。预测形变场$\phi$的质量通过雅克比行列式$det(\nabla\phi^{-1}(x))$为负数的位置的数量来进行评估,即$\mathcal{N}:=\sum \delta\left(\operatorname{det}\left(D \phi^{-1}\right)<0\right)$。
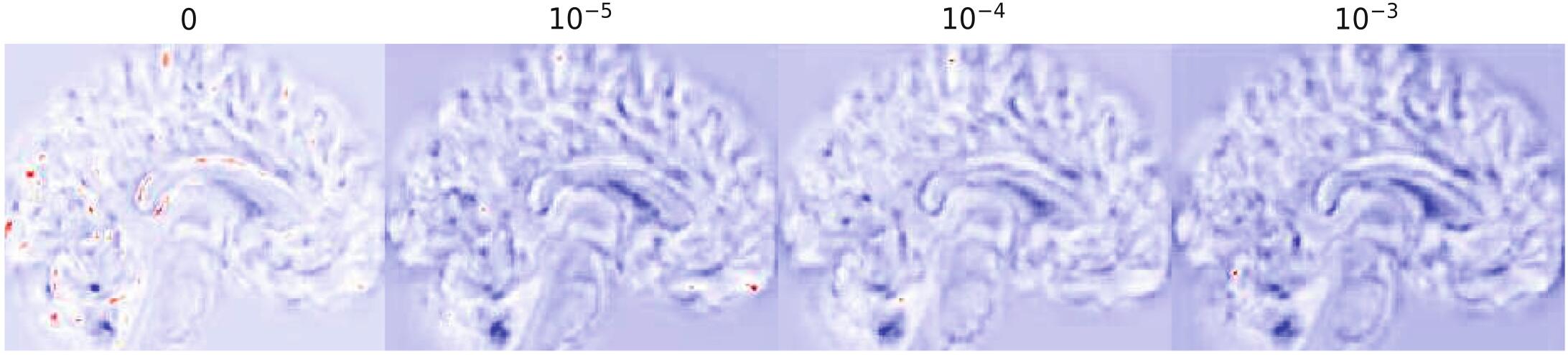
上图是FAIM预测的形变场对应的雅克比行列式图,四张图分别表示在$\beta$不同取值下的情况,红色的部分表示有重叠(行列式值为负数),蓝色的部分表示行列式值为正。在正则项没有使用的时候,即$\beta=0$时,形变场中有很多位置的雅克比行列式是负数,当$\beta=10^{-5}$时,该数量就会骤减。
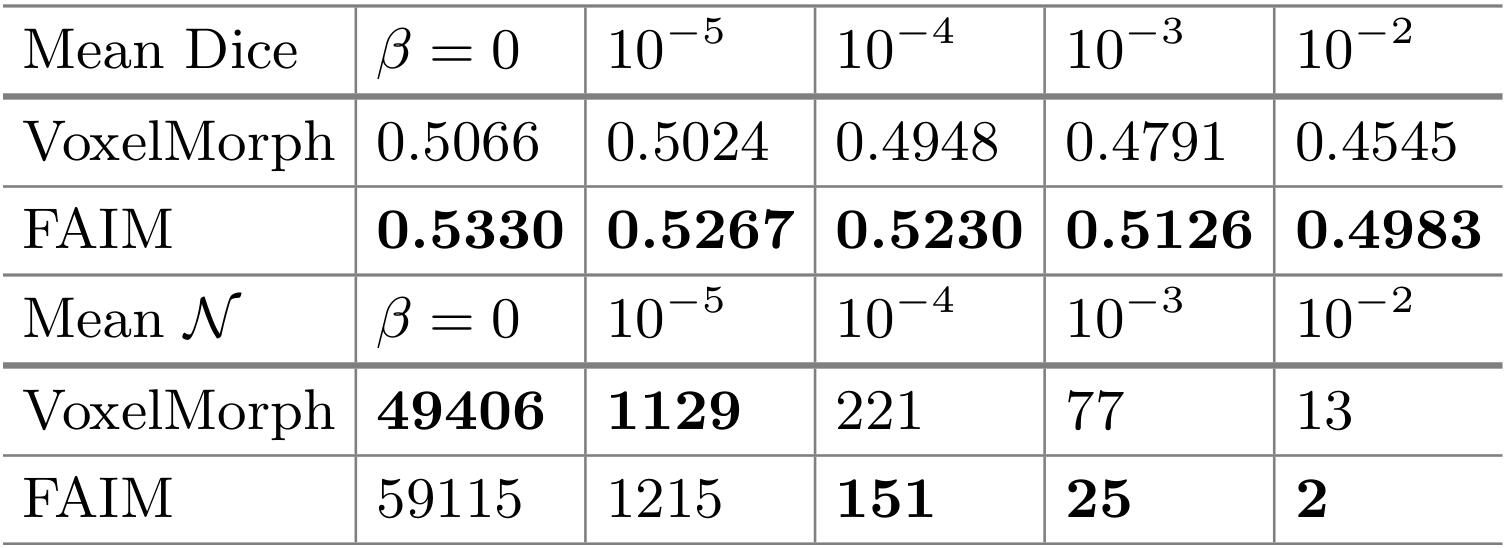
上图是不同$\beta$取值情况下,VoxelMorph和FAIM模型配准的Dice和$N$的均值情况。
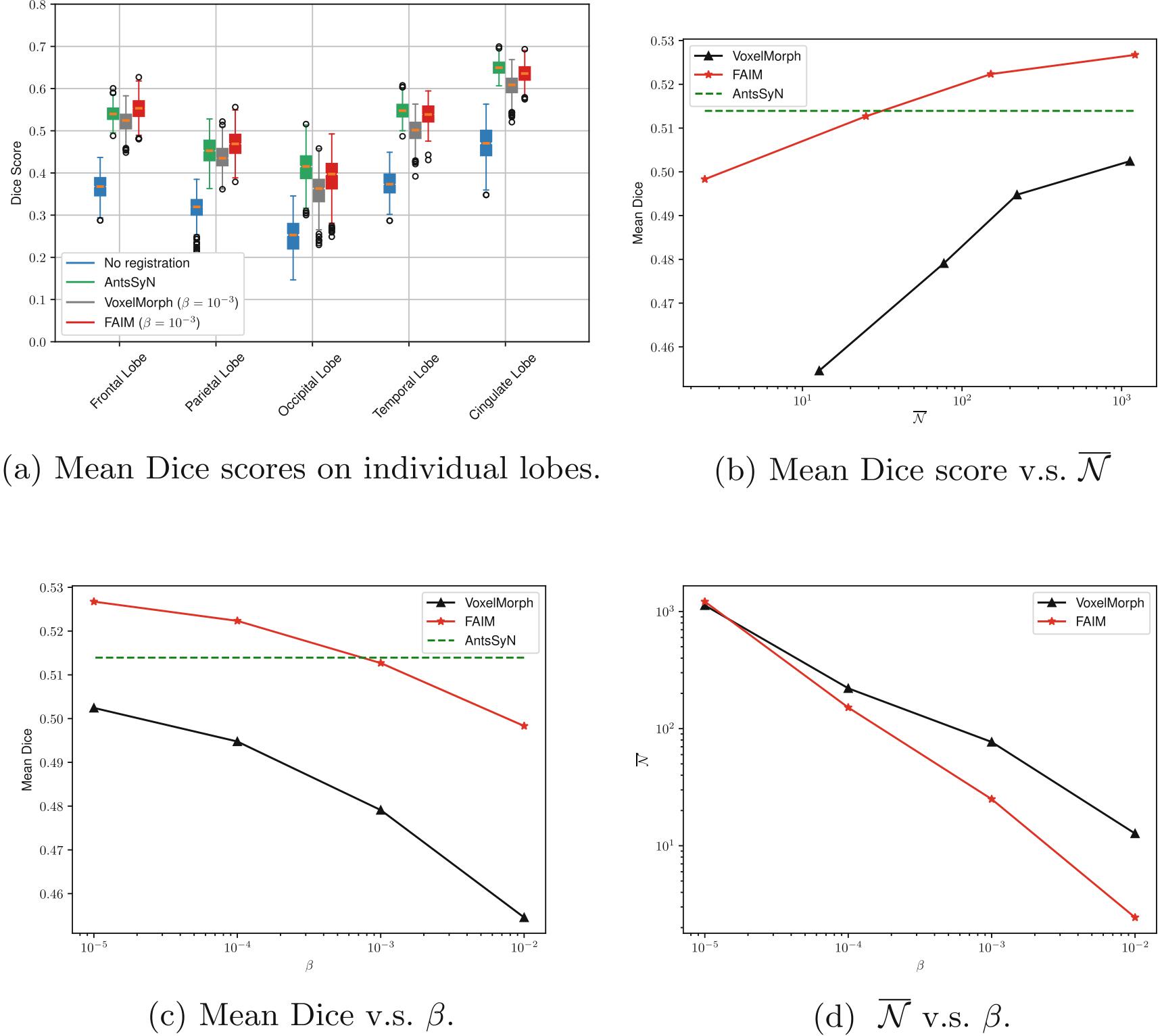
为了研究网络怎么平衡高准确率和第重叠区域,在上图(b)中绘制了平均dice得分与重叠位置的平均数量。
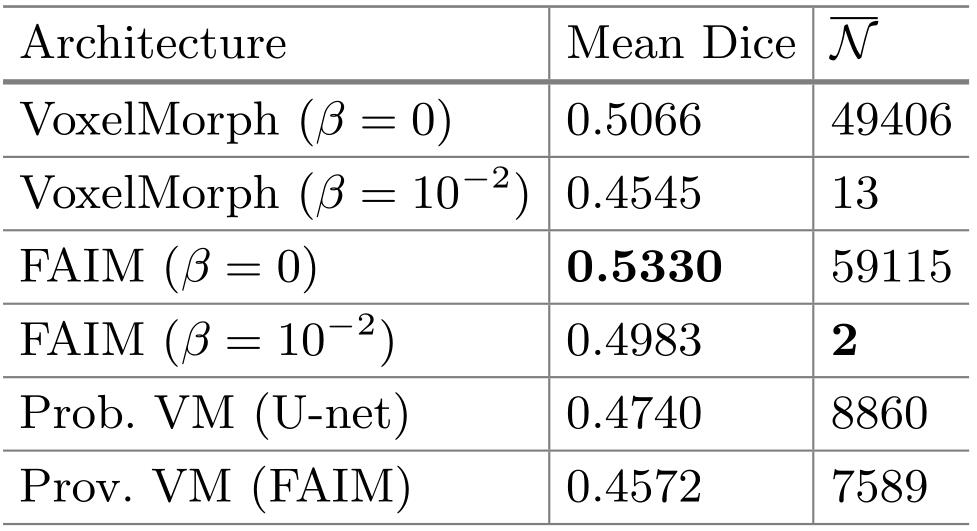
Probabilistic VoxelMorph不是使用显式的损失来控制重叠,而是在一个积分层(integration layer)使用展开和缩放(square and scale)算法来迭代计算由UNet产生的速度场的组成,以得到最终的变形。此外还将Prob-VoxelMorph的backbone从UNet改成了FAIM,来验证backbone的不同而造成的影响,可以发现backbone的不同不会导致太大的差异。上图对比了VM、FAIM、以UNet为backbone的Prob-VM和以FAIM为backbone的Prob-VM。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/08/04/FAIM/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


