本文是文章《Inverse-Consistent Deep Networks for Unsupervised Deformable Image Registration》的阅读笔记。
过去基于学习的配准方法忽略了图像之间转换的逆一致性,并且形变场只被要求局部平滑,不能完全避免形变场的重叠。基于以上两点,提出了一个用于无监督图像配准的逆一致性网络模型ICNet,同时提出了“反重叠约束”来避免形变场的重叠。
一、配准问题
用$S$表示源图像(浮动图像),$T$表示目标图像(固定图像),$F_{ST}$表示从图像$S$变到图像$T$的位移场,配准问题可看作是解决以下优化问题:
$$
\mathcal{F}(\mathbf{S}, \mathbf{T})=\mathcal{L}{\text {similar}}\left(\mathbf{T}, \Phi\left(\mathbf{S}, \mathbf{F}{S T}\right)\right)+\mathcal{R}\left(\mathbf{F}{S T}\right)
$$
其中$\Phi$表示转换操作,$\Phi(S,F{ST})$表示根据位移场$F_{ST}$变形后的源图像,第一项表示图像之间的相似度,第二项是正则化项。
传统的基于学习的配准算法输出的转换,即位移场或流(flow)通常是不对称的,也就是说图像之间变换的逆一致性被忽略了。这里的逆一致性简单来说就是在配准时不仅要将图像$A$配准到图像$B$,同时还应该将图像$B$配准到图像$A$。

上图中分别是当形变场平滑约束使用较大权重和较小权重时的结果。
二、网络结构
在本文中用$A$表示源图像,$B$表示目标图像,$F_{AB}$表示从图像$A$到图像$B$的位移场,$F_{BA}$表示从图像$B$到图像$A$的位移场。位移场中每个元素是一个三维向量,分别表示在$x,y,z$轴方向的体素从原图像到新图像的位移。变形后的$A$和$B$被记作$\tilde{A}$和$\tilde{B}$。

上图中图(a)是ICNet的网络结构,图(b)是FCN的网络结构,图(c)是逆网络的结构。
在ICNet中使用两个FCN来预测两个位移场$F_{AB}$和$F_{BA}$。第一个FCN的目的是根据位移场$F_{AB}$将$A$朝$B$对齐,并得到变形后的图像$\tilde{A}$,第二个FCN的目的是根据位移场$F_{BA}$将$B$朝$A$对齐,并得到变形后的图像$\tilde{B}$。两个FCN的结构相同,参数共享,说白了就是用的同一个FCN。
FCN采用的和UNet类似的结构,n表示FCN中一开始的过滤器的个数,收缩路径的每一步包括一个$3\times3\times3$,步长为1的卷积操作和一个$3\times3\times3$,步长为2的卷积操作(用作下采样)。扩张路径的每一步包括一个$2\times2\times2$,步长为2的反卷积操作用作上采样,并跟着一个拼接操作,将收缩路径和扩张路径的特征图拼接,然后是一个$3\times3\times3$,步长为1的卷积。每个卷积操作后都跟着一个ReLU激活函数,在FCN的最后一层,先用Tanh激活函数将输出值的范围限制在[-1,1],然后再乘以$\tau$,将输出值限制在$[-\tau, \tau]$,$\tau$表示最大的位移。
使用网格采样模块(即空间变换网络,STN)获得变形后的图像,STN采用的是双线性插值,所以是可微的。此外,使用一个逆网络来基于逆一致性损失$Loss_{inv}1和Loss_{inv}2$,并根据位移场$F_{AB}$生成一个估计的逆位移场$\tilde F_{BA}$。具体的,使用网格采样策略来基于$F_{AB}$和$-F_{AB}$生成逆位移场$\tilde F_{BA}$。对于位移场$F_{AB}$,首先获得它的负的位移场$-F_{AB}$,然后将它们喂入STN中获得估计的逆位移场$\tilde F_{BA}$。同理可获得$\tilde F_{AB}$。
三、损失函数
1. 逆一致性约束
逆一致性约束定义如下:
$$
\mathcal{L}{i n v}=\left|\mathbf{F}{A B}-\widetilde{\mathbf{F}}{A B}\right|{F}^{2}+\left|\mathbf{F}{B A}-\widetilde{\mathbf{F}}{B A}\right|{F}^{2}\
\begin{array}{l}
\widetilde{\mathbf{F}}{A B}=\mathcal{G}\left(\mathbf{F}{B A},-\mathbf{F}{B A}\right) \
\widetilde{\mathbf{F}}{B A}=\mathcal{G}\left(\mathbf{F}{A B},-\mathbf{F}_{A B}\right)
\end{array}
$$
其中,$\mathcal{G}$是STN产生的映射,$||\cdot||_F$表示矩阵的弗罗贝纽斯(Frobenius)正则。
2. 反重叠约束
反重叠约束:
$$
\begin{aligned}
\left.\mathcal{L}{\text {ant }}=\Sigma{p \in \Omega} \Sigma_{i \in{x, y, z}}\right. & \delta\left(\nabla \mathbf{F}{A B}^{i}(p)+1\right)\left|\nabla \mathbf{F}{A B}^{i}(p)\right|^{2} \
&+\delta\left(\nabla \mathbf{F}{B A}^{i}(p)+1\right)\left|\nabla \mathbf{F}{B A}^{i}(p)\right|^{2}
\end{aligned}
$$
其中,$\nabla F^i_{AB}(p)$是位移场$F_{AB}$中体素$p$在第$i$个轴的梯度,$\delta(Q)$是用来惩罚位移场中有重叠的位置的梯度的指示函数。如果$Q\le0,\delta(Q)=|Q|$,反之,$\delta(Q)=0$。
如果在位置$p$沿着第$i$个轴处有重叠,即$\nabla F^i_{AB}(p)+1\le0$,则增加惩罚$\nabla F^i_{AB}(p)+1$在该位置的梯度上,以让梯度变得小,反之,如果$\nabla F^i_{AB}(p)+1>0$,即没有重叠,则不做惩罚。
3. 平滑约束
平滑约束的定义如下:
$$
\mathcal{L}{s m o}=\Sigma{p \in \Omega}\left(\left|\nabla \mathbf{F}{A B}(p)\right|{2}^{2}+\left|\nabla \mathbf{F}{B A}(p)\right|{2}^{2}\right)
$$
其中,$\nabla F_{AB}(p)$是体素$p$处的位移场$F_{AB}$的梯度,$\nabla F_{BA}(p)$是体素$p$处的位移场$F_{BA}$的梯度,$||\cdot||_2$表示向量的$L_2$正则。
4. 图像相似性度量
使用MSD(mean squared distance)作为图像的相似性度量,该损失用来衡量图像之间的大小差异,其定义如下:
$$
\mathcal{L}{s i m}=|\mathbf{B}-\widetilde{\mathbf{A}}|{F}^{2}+|\mathbf{A}-\widetilde{\mathbf{B}}|{F}^{2}
$$
其中,$\widetilde{\mathbf{A}}=\mathcal{G}\left(\mathbf{F}{A B}, \mathbf{A}\right)$,$\widetilde{\mathbf{B}}=\mathcal{G}\left(\mathbf{F}_{B A}, \mathbf{B}\right)$,$\mathcal{G}$是由STN得到的映射函数。
5. 总损失
ICNet的总损失如下:
$$
\begin{aligned}
\mathcal{L}(\mathbf{A}, \mathbf{B}) &=\mathcal{L}{s i m}+\alpha \mathcal{L}{s m o} \
&+\beta \mathcal{L}{i n v}+\gamma \mathcal{L}{a n t}
\end{aligned}
$$
其中$\alpha,\beta,\gamma$是平衡因子。
四、实验
1. 预处理
在图像的预处理阶段,要对图像做空间正则化和灰度值正则化。空间正则化包括颅骨去除、小脑移除,并将它们线性对齐到Colin27模板,然后将图像重采样到相同的分辨率($1mm\times1mm\times1mm$),再将其剪裁到相同大小($144\times192\times160$)。灰度值正则化包括先使用直方图匹配算法将灰度直方图匹配到Colin27模板,并进行z-score正则化(减均值,除以标准差),以让图像的均值和标准差分别为0和1。
2. 实验设置
在实现时,使用Adam作为优化器,学习率为$5e^{-4}$,使用ADNI-1数据集,随机划分10%的数据作为验证集,剩余的作为训练集,迭代次数为4w次。
在实验中进行两个任务来衡量配准的效果:脑组织分割和解剖学地标检测;实验使用的baseline有Demons、SyN和基于无监督学习的深度学习方法DL(使用MMSE,minimum mean squared error作为相似性度量)。将不适用逆一致性约束的ICNet记为ICNet-1,将不使用反重叠约束的ICNet记为ICNet-2。
在ADNI-2数据集中选用5个MR图像作为图谱,使用多数投票策略进行基于多图谱的分割,以进行脑组织分割任务。在地标检测中,每个图谱中的地标先被映射到指定的测试图像,因此给定测试图像,就得到了5个变形后的地标位置(对于每个地标来说),然后计算5个位置的平均位置得到最终的地标位置。
在ICNet中,$\gamma$被设置为$10^5$,$\alpha,\beta$被限制在$[10^{-5},10^{-4},…,10^5]$范围内。在ICNet-1中$\beta=0,\gamma=10^5$,在ICNet-2中$\gamma=0$。FCN一开始的过滤器的通道数$n=8$,$\tau=7$。在脑组织分割任务中,使用的度量指标为DSC(dice similarity coefficient)、SEN(sensitivity)、PPV(positive predictive value)、ASD(average symmetric surface distance)、HD(Hausdorff distance)。在地标检测任务中,通过计算预测地标位置和ground truth位置之间的欧几里得距离来计算地标检测的误差。ACC、SEN、PPV越高说明效果越好,ASD、HD和检测误差越小说明效果越好。
3. 实验结果
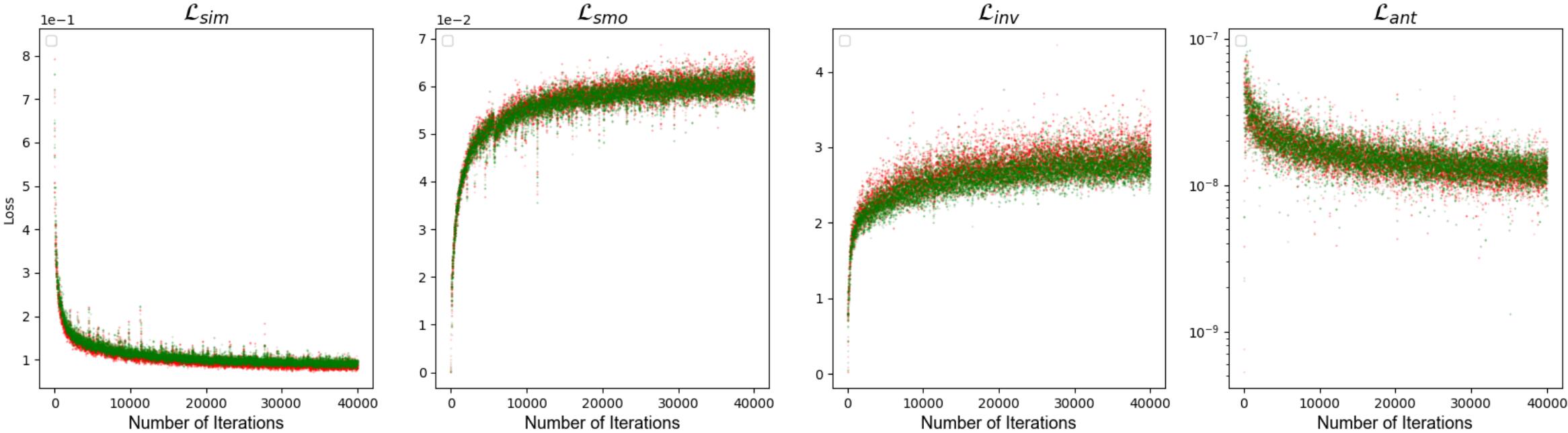
上图是训练和验证的损失,红色的表示训练损失,绿色的表示验证损失,四个图分布是相似度、平滑度、逆一致性和反重叠损失。
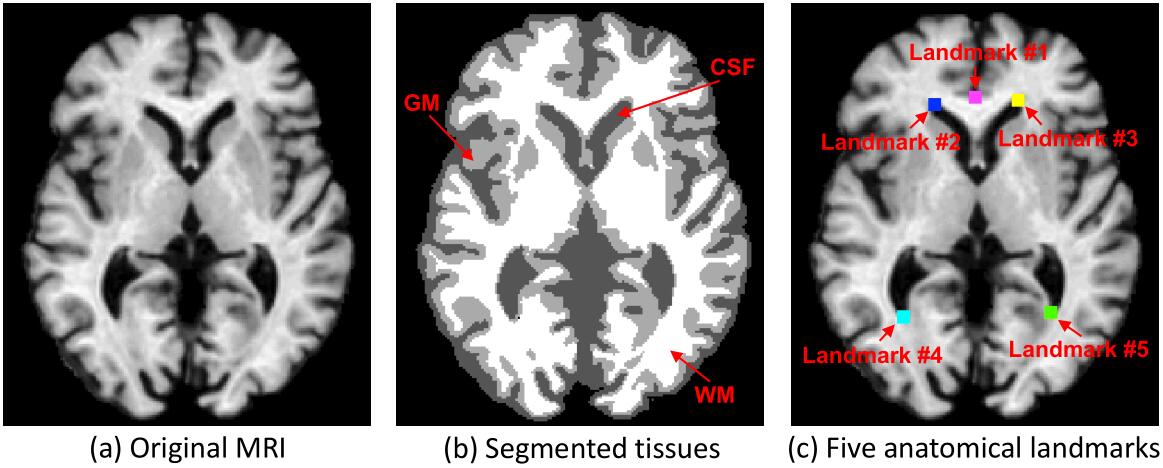
上图分别表示原图;三种分割组织图,其中CSF是脑脊液,GM是灰质,WM是白质;五个解剖学地标(用不同颜色的块表示)。
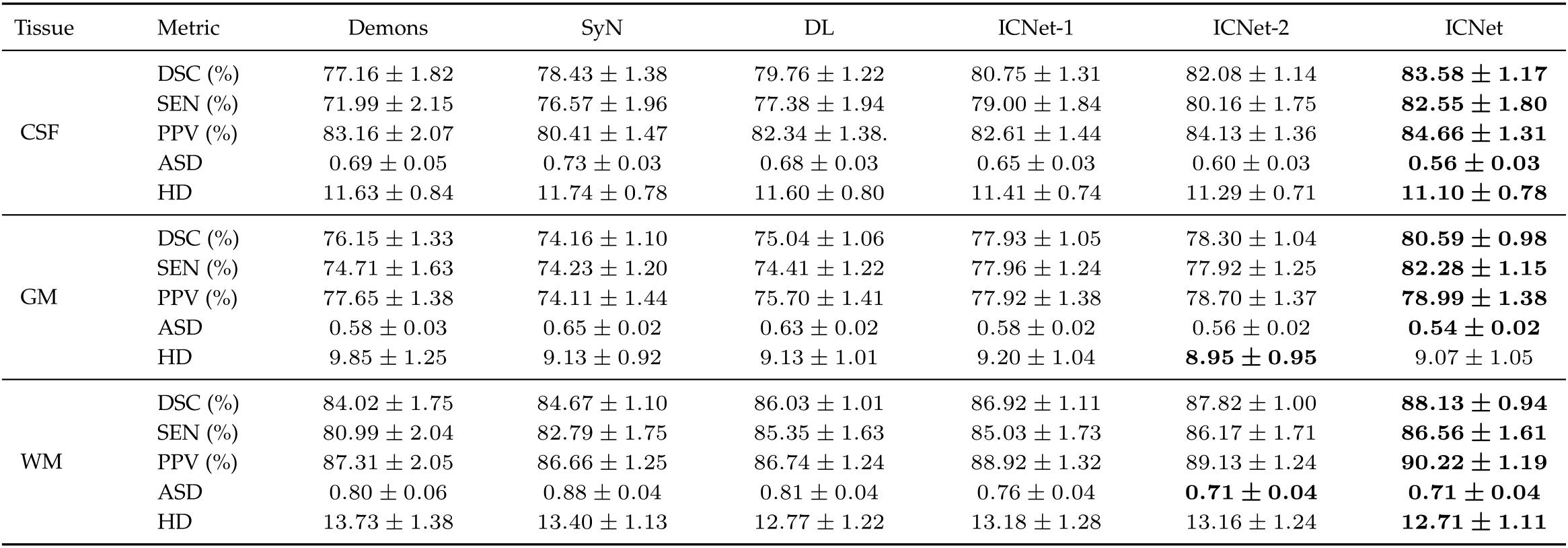
上图是三个脑组织的分割结果,可以发现ICNet在绝大多数分割和衡量指标上都达到了最优结果。

上图是六种算法的配准结果,红色和黄色箭头分别表示左右颞平面。

上图是六个算法在地标检测时的误差,ICNet在3个地标和平均误差中都取得了最优效果。

上图是各个算法的测试时间对比。
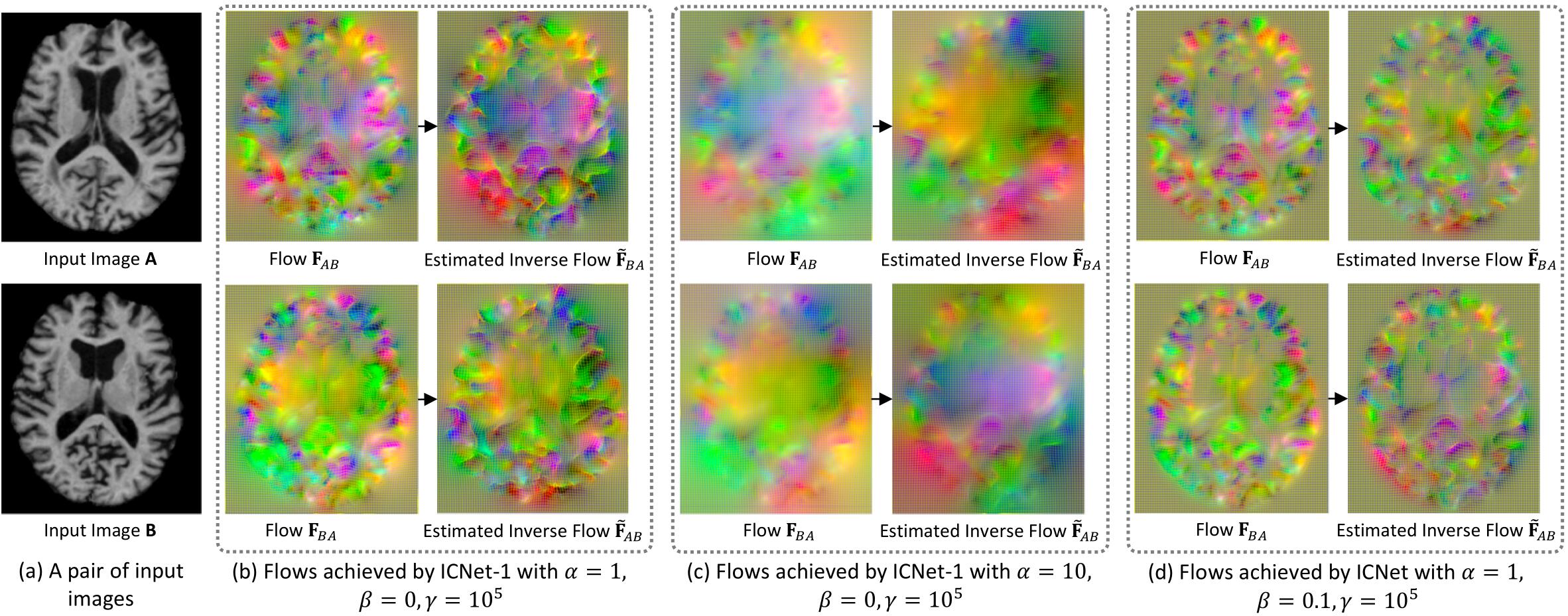
上图是不同权重系数下的形变场情况。
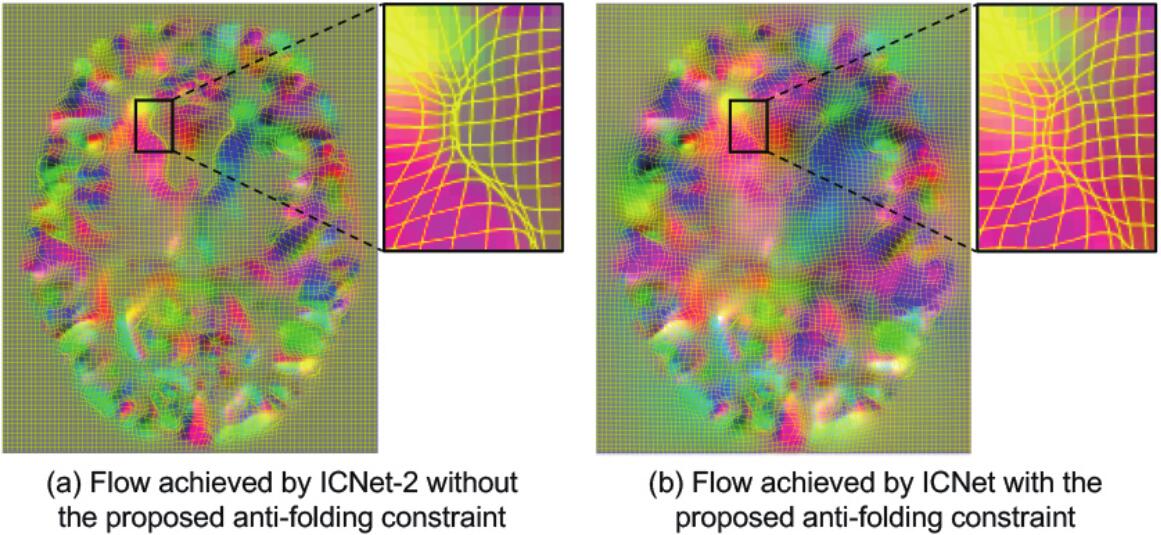
上图是两种模型不使用反重叠约束的情况。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/07/29/ICNet/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


