本文是论文《Fast Symmetric Diffeomorphic Image Registration with Convolutional Neural Networks》的阅读笔记。文章中有很多关于数学的描述,包括微分同胚、雅克比矩阵没有看懂,所以这部分内容有所残缺,建议读者直接阅读原文。
一、摘要
由于之前的方法忽略了形变场的拓扑保持(topology preservation),并且形变场的平滑性只由全局平滑能量函数来约束,文章提出了一个名为SYMNet的无监督对称图像配准模型,该模型同时估计正向和反向的变换。
基于深度学习的配准方法中实质微分同胚性(substantial diffeomorphic properties)没有得到保证,即忽略了变换的拓扑保持和可逆性。模型的输出是一对微分同胚映射,用来将输入图像从两条测地线(geodesic path)映射到两幅图像的中间地带(middle ground)。微分同胚是可微的映射,并且存在可微的逆。
文章的主要贡献有:
- 提出了一个快速对称微分同胚图像配准方法来保证变换的拓扑保持和可逆性;
- 提出了新的方向一致性正则化,用负的Jacobian行列式来惩罚局部区域;
- 文章提出的范式和目标函数很容易在其他地方应用。
二、 可变形图像配准
可变形图像(deformable image)配准的目标是建立起图像对之间的一个非线性关系,并且估计一个对齐两张图像的非线性转换。
可变形图像配准指的是将浮动图像变形以对齐到固定图像的过程,在该过程中两幅图像之间的相似性得到最大化。可变形图像配准是一个非线性配准过程用来建立浮动图像和固定图像之间的密集的体素级的非线性空间关系(dense voxel-wise non-linear spatial correspondence)。
用$F$和$M$分别表示固定图像和浮动图像,$\phi$来表示形变场,可变形图像配准过程可以表示为:
$$
\phi^{}=\underset{\phi}{\arg \min } \mathcal{L}{s i m}(F, M(\phi))+\mathcal{L}{r e g}(\phi)
$$
其中$\phi^{}$表示最优的形变场,$\mathcal{L}{sim}(\cdot,\cdot)$表示不相似性函数,$\mathcal{L}{seg}(\cdot)$表示平滑正则函数,$M(\phi)$表示变形后的浮动图像。
三、相关工作
1. 微分同胚配准
当前的配准方法通常是将位移场$u$参数化,形变场和位移场的关系为:$\phi(x)=x+u(x)$,其中$x$是恒定变换。这种方式虽然简单,但是对于大的变形来说可能对应的位移场并不存在,所以文章使用的是带有静态速度场的微分同胚变形模型。微分同胚是可微和可逆的,这就保证了平滑的一对一的映射,同时也保留了拓扑性。微分同胚形变场$\phi_t$可以由速度场来生成:
$$
\frac{d \phi_{t}}{d t}=\boldsymbol{v}^{t}\left(\phi^{t}\right)=\boldsymbol{v}^{t} \circ \phi^{t}
$$
其中$\circ$是复合运算符(composition operator),$v^t$表示时间$t$时刻的速度场,$\phi^0=Id$是恒等变换。
形变场可以表示为李代数的一员,并将其指数化以产生时间为1的变形$\phi^{(1)}$,即李群$\phi^{(1)}=\exp(v)$的一员。这表示指数化的流场使得映射是微分同胚和可逆的。给定初始形变场$\phi^{\left(1 / 2^{T}\right)}=x+v(x) / 2^{T}$,其中$T$表示总的时间,那么,$\phi^{(1/2)}$可以通过重现(recurrence)得到:$\phi^{\left(1 / 2^{t-1}\right)}=\phi^{\left(1 / 2^{t}\right)} \circ \phi^{\left(1 / 2^{t}\right)}$。
2. 基于学习的配准
大多数有监督的配准方法采用ground truth形变场或分割图来指导学习过程。文献11(DIRNet)证明了在无监督配准中采用互相关作为相似度评价指标的有效性,文献5(VoxelMorph)通过$L_2$正则损失使得形变场平滑,文献9提出了一个概率微分同胚配准模型。
四、方法
大多数基于学习的配准方法都是只从浮动图像映射到固定图像,而忽略了其逆映射(从固定图像映射到浮动图像)。让$X$,$Y$表示两个3D图像,可变形配准问题可以参数化为一个方程:$f_{\theta}(X, Y)=\left(\phi_{X Y}^{(1)}, \phi_{Y X}^{(1)}\right)$,其中$\theta$表示CNN的参数,$\phi_{X Y}^{(1)}=\phi_{X Y}(x, 1)$和$\phi_{Y X}^{(1)}=\phi_{Y X}(y, 1)$分别表示时间为1的从位置$x\in X$变形到$y\in Y$和从位置$y\in Y$变形到$x\in X$的微分同胚形变场。
文章提出分别学习两个时间为0.5的将$X$和$Y$变形到它们的平均大小$M$的形变场,模型收敛之后,时间为1的将$X$变形到$Y$和将$Y$变形到$X$的形变场就可以通过结合两个估计的时间为0.5的形变场而得到了。从$X$到$Y$的变形可以结构为:$\phi_{X Y}^{(1)}=\phi_{Y X}^{(-0.5)}\left(\phi_{X Y}^{(0.5)}(x)\right)$,从$Y$到$X$的变形可以结构为:$\phi_{XY}^{(1)}=\phi_{X Y}^{(-0.5)}\left(\phi_{Y X}^{(0.5)}(y)\right)$。因此方程$f_\theta$可以重写为:$f_{\theta}(X, Y)=\left(\phi_{Y X}^{(-0.5)}\left(\phi_{X Y}^{(0.5)}(x)\right), \phi_{X Y}^{(-0.5)}\left(\phi_{Y X}^{(0.5)}(y)\right)\right)$。
1. 对称微分同胚神经网络
将方程$f_\theta$参数化为一个全卷积网络(FCN)、缩放层、squaring层和可微的空间变换器(STN),$\phi_{XY}^{(0.5)}$和$\phi_{YX}^{(0.5)}$使用缩放和squaring方法通过估计的速度场$v_{XY}$和$v_{YX}$来计算。FCN网络的结构类似于UNet,是一个5层的编码器-解码器结构,并且有跳跃连接。FCN以拼接的2通道的图像作为输入,以2个密集的(dense)、非线性的速度场$v_{XY}$和$v_{YX}$作为输出。在编码器的每一层,都有两个卷积核大小为$3\times3\times3$,步长分别为1和2的卷积层。在解码器的每一层采用步长为1的卷积核大小分别为$3\times3\times3$的卷积层和步长为1,卷积核为$2\times2\times2$的反卷积层。在解码器的最后两层是卷积核大小为$5\times5\times5$,步长为1的卷积层,并且跟着一个softsign激活函数($\operatorname{softsign}(x)=\frac{x}{1+|x|}$),然后乘以常数$c$,用来产生两个速度场。乘以常数$c$是为了让速度场的范围在$[-c,c]$之间。实际操作时$c=100$。除了最后一个卷积层,FCN的每一个卷积层后面都跟着一个ReLU激活函数。
此外,使用空间变换器(STN)实现缩放层和squaring层,并用它对预测的速度场进行积分。
特别的给定时间步长$T$,初始化$\phi_{X Y}^{\left(1 / 2^{T}\right)}=x+\boldsymbol{v}{X Y}(x) / 2^{T}$和$\phi{YX}^{\left(1 / 2^{T}\right)}=x+\boldsymbol{v}_{YX}(x) / 2^{T}$,通过重现$\phi\left(1 / 2^{t-1}\right)=\phi^{(1 / t)} \circ \phi^{(1 / t)}$计算时间为0.5的形变场,直到$t=1$。
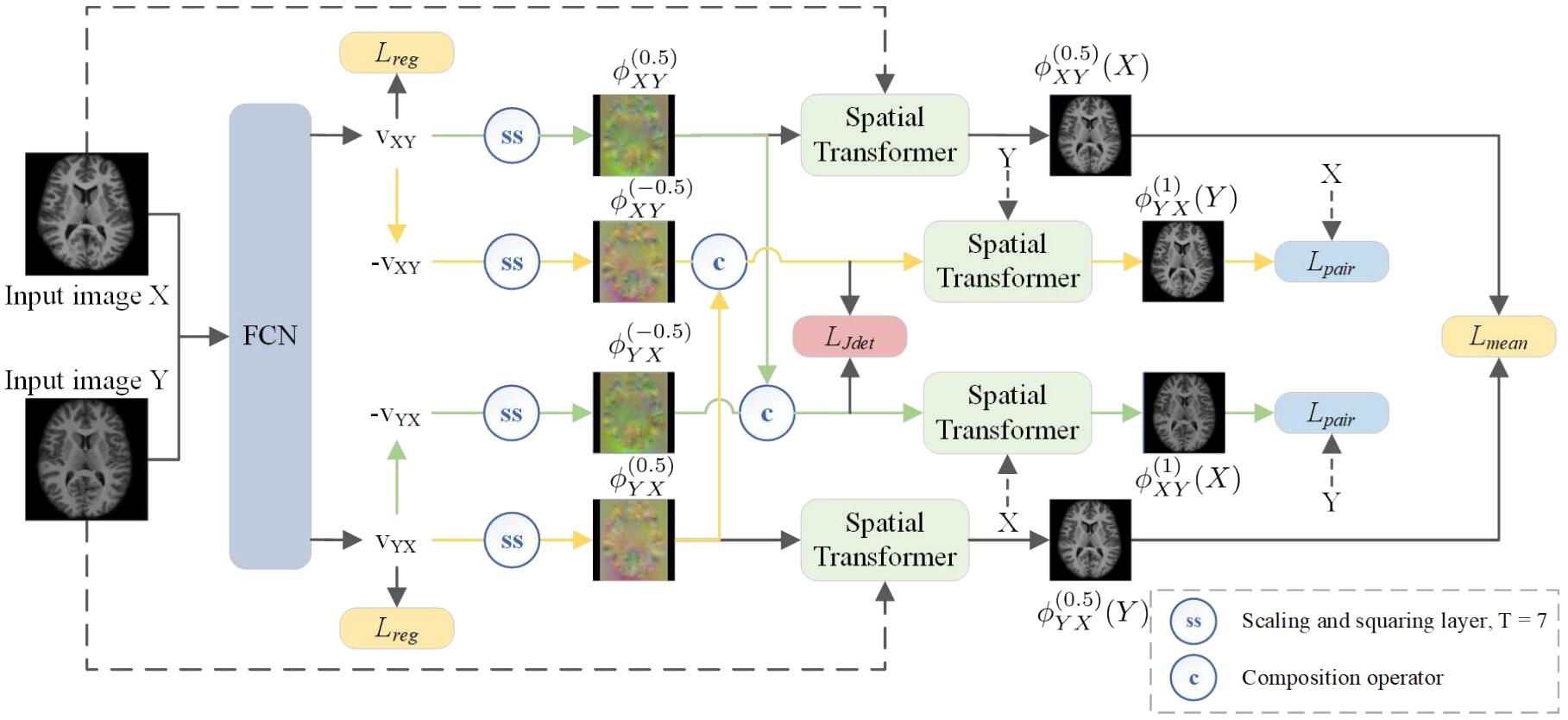
上图是模型的结构示意图,使用FCN来学习从$X,Y$到他们平均大小$M$的对称的时间为0.5的形变场,绿色的路径表示从$X$到$Y$的变换,黄色的路径表示从$Y$到$X$的变换,为了简介没有在图中画出$\mathcal{L}_{mag}$损失。
据我自己的理解,$\phi^{(0.5)}{YX}$表示从图像$Y$到$X$的形变场,$\phi^{(0.5)}{XY}$表示从$X$到$Y$的形变场,上图中的ss表示softsign激活函数,c表示常数,这两者上面提到过。而$\phi^{(-0.5)}{YX}$表示从$\phi^{(0.5)}{YX}$得到的逆形变场,即从$X$到$Y$的形变场,具体操作是先对$V_{YX}$取相反数,得到$-V_{YX}$,然后经过softsign激活函数,得到逆形变场$\phi^{(-0.5)}_{YX}$,然后乘以常数c,然后和图像$X$一同送入ST中,得到变换后的图像。另一个逆形变场的生成过程与之类似。
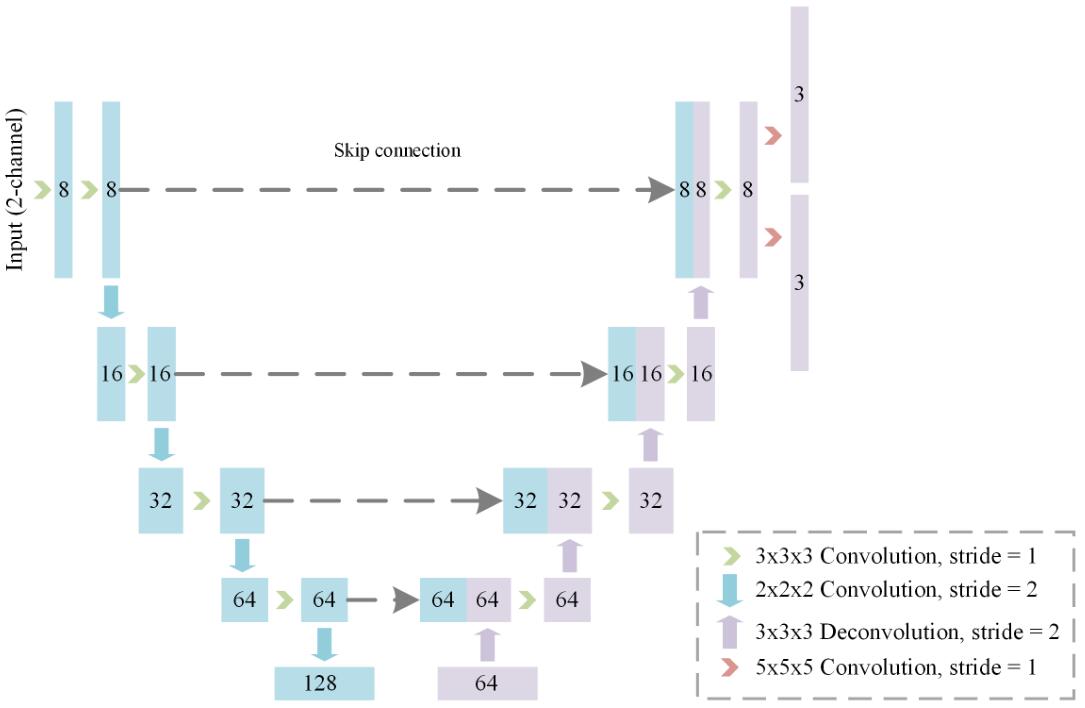
上图是FCN网络的结构示意图。
2. 对称相似性
$\mathcal{L}{mean}$是对称平均形状相似性损失,$\mathcal{L}{sim}$是图像的相似性损失,有很多相似性度量,比如正则化的互相关NCC、均方误差MSE、距离的平方和SSD和互相关MI,这里选用的是NCC。让$I$和$J$表示两个输入图像,$\bar{I}(x)$和$\bar{J}(x)$分别是$I$和$J$在位置$x$的局部均值,局部均值通过以$x$为中心,大小为$w^3$,$w=7$的窗口来计算。NCC的定义如下:
$$
\begin{array}{l}
N C C(I, J)=
\sum_{x \in \Omega} \frac{\sum_{x_{i}}\left(I\left(x_{i}\right)-\bar{I}(x)\right)\left(J\left(x_{i}\right)-\bar{J}(x)\right)}{\sqrt{\sum_{x_{i}}\left(I\left(x_{i}\right)-\bar{I}(x)\right)^{2} \sum_{x_{i}}\left(J\left(x_{i}\right)-\bar{J}(x)\right)^{2}}}
\end{array}
$$
其中$x_i$表示以$x$为中心的窗口内的位置。
$\mathcal{L}{sim}$的表示如下:
$$
\mathcal{L}{s i m}=\mathcal{L}{\text {mean}}+\mathcal{L}{\text {pair}}
$$
$$
\mathcal{L}{\text {mean}}=-N \operatorname{CC}\left(X\left(\phi{X Y}^{(0.5)}\right), Y\left(\phi_{Y X}^{(0.5)}\right)\right)
$$
$$
\mathcal{L}{\text {pair}}=-N C C\left(X\left(\phi{X Y}^{(1)}\right), Y\right)-N C C\left(Y\left(\phi_{Y X}^{(1)}\right), X\right)
$$
其中,$\mathcal{L}{mean}$用来衡量$X$和$Y$之间的不相似性,它们朝向平均大小$M$,$\mathcal{L}{pair}$衡量变形后的$X$和$Y$以及变形后的$Y$和$X$之间的不相似性。
3. 局部方向一致性
全局正则化会使配准的精度降低,实际上全局正则化不能保证变换的拓扑保持,为了解决这个问题,提出了可选性雅可比行列式正则,以促进预测形变场的局部的方向一致性。可选性雅克比行列式正则损失为:
$$
\mathcal{L}{J d e t}=\frac{1}{N} \sum{p \in \Omega} \sigma\left(-\left|J_{\phi}(p)\right|\right)
$$
其中$N$表示$|J_\phi|$中元素的总数量;$\sigma(\cdot)$表示激活函数,这里用的是$\sigma(\cdot)=\max(0,\cdot)$,作用等同于ReLU;$|J_\phi(\cdot)|$表示在位置$p$处形变场$\phi$的雅克比行列式,其公式如下:
$$
J_{\phi}(p)=\left(\begin{array}{lll}
\frac{\partial \phi_{x}(p)}{\partial x} & \frac{\partial \phi_{x}(p)}{\partial y} & \frac{\partial \phi_{x}(p)}{\partial z} \
\frac{\partial \phi_{y}(p)}{\partial x} & \frac{\partial \phi_{y}(p)}{\partial y} & \frac{\partial \phi_{y}(p)}{\partial z} \
\frac{\partial \phi_{z}(p)}{\partial x} & \frac{\partial \phi_{z}(p)}{\partial y} & \frac{\partial \phi_{z}(p)}{\partial z}
\end{array}\right)
$$
但是并不是用可选性雅克比行列式正则损失代替原来的全局正则化,而是同时使用两者,以产生平滑且拓扑保持的变换。
接着,使用$\mathcal{L}{r e g}=\sum{p \in \Omega}\left(\left|\nabla \boldsymbol{v}{X Y}(p)\right|{2}^{2}+\left|\nabla \boldsymbol{v}{Y X}(p)\right|{2}^{2}\right)$来加强速度场的平滑,还通过幅值约束(magnitude constraint)$\mathcal{L}{m a g}=\frac{1}{N}\left(\left|\boldsymbol{v}{X Y}\right|{2}^{2}-\right.\left.\left|\boldsymbol{v}{Y X}\right|{2}^{2}\right)$来避免在路径上的偏移。所以总的损失函数为:
$$
\mathcal{L}(X, Y)=\mathcal{L}{s i m}+\lambda_{1} \mathcal{L}{J d e t}+\lambda{2} \mathcal{L}{r e g}+\lambda{3} \mathcal{L}_{m a g}
$$
五、实验
在T1权重的脑部MRI数据集OASIS上做了基于图谱的配准实验,先将所有图像重采样到$256\times256\times256$大小,然后使用FreeSurfer做标准的预处理,包括运动校正、去除头骨、仿射空间归一化和皮质下结构分割。然后将图像裁剪为$144\times192\times160$大小。并将数据集划分为255、20、150分别作为训练集、验证集和测试集。随机从测试集选择5个MR图像作为图谱。
使用Dice相似系数(DSC)和雅克比行列式$|J_\phi|$作为衡量标准。DSC的取值范围是[0,1],配准的越好对应的DSC值越大。雅克比行列式可以捕捉形变场的局部行为。选用ANTs包中的SyN、VoxelMorph(VM)和DIF-VM作为baseline。使用SGD优化器,学习率为$1e^{-4}$,动量为0.9,$\lambda_1=1000,\lambda_2=3,\lambda_4=0.1$。
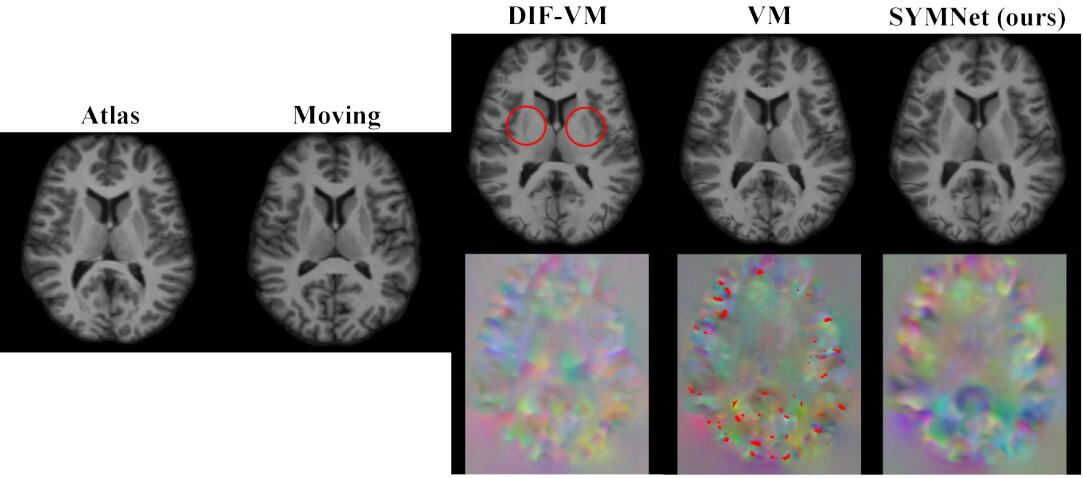
上图是SYMNet与baseline模型的配准结果对比。

上图是平均DSC值(越高越好)和非正雅克比行列式的平均体素数(越低越好),可以发现SYMNet在DSC上取得最好的效果,在$|J_\phi|$上效果次优。
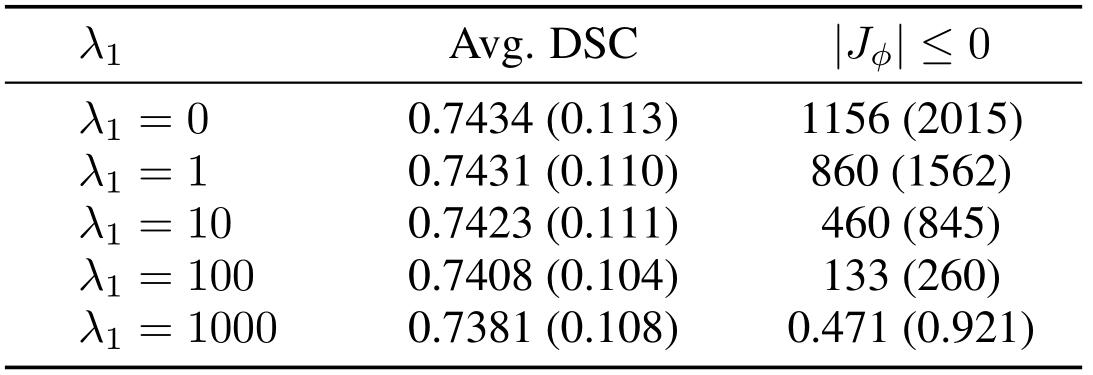
上表展示了局部方向一致性损失的影响。

上表对比了各种模型运行所需要的时间,可以发现SYMNet所需时间最短。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/07/24/SYMNet/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


