本文是论文《A Taxi Order Dispatch Model based On Combinatorial Optimization》的阅读笔记。
一、摘要
传统的订单分配系统都是最大化每个订单的司机接受率,通常会对于每个订单寻找一个最近的司机,这导致了较低的全局成功率,并且订单分配的时间较长。文章提出了一个目的地预测模型,可以在用户一打开APP的时候就对用户可能去的目的地进行预测,本文提出的模型不仅在全局成功率,而且在用户等待时间、接车距离等方面都获得了很大的提升。
在本文提出的模型中,会把一个订单分配给多个司机,当第一个接受订单的司机获得该订单,如果没有被接受,则进入下一轮直到订单被接受或被取消。
一个订单主要有三个重要的属性:出发时间、出发位置和目的地位置,文章提出的贝叶斯目的地预测模型会使用用户的历史出行目的地作为目的地预测的候选集合。贝叶斯目的地预测模型以出发时间、出发位置和目的地位置为输入,并将其看作一个三元的高斯分布,然后会生成每个目的地的概率,并按照概率大小给出一个预测目的地的列表。
二、订单分配系统
1. 记号
- $E_{SR}$:成功率
- $N$:订单数
- $M$:司机数
订单分配结果可以用一个矩阵来表示:
$$
\left(\begin{array}{ccc}a_{11} & \cdots & a_{1 M} \ \vdots & a_{i j} & \vdots \ a_{N 1} & \cdots & a_{N M}\end{array}\right), where\quad 1 \leq i \leq N, 1 \leq j \leq M\
and\quad a_{i j}=\left{\begin{array}{ll}1 & \text { order } i \text { is dispatched to driver } j \ 0 & \text { order } i \text { is not dispatched to driver } j\end{array}\right.
$$
一个司机只能同时接一个订单,而一个订单可以分配给多个司机,所以上式满足约束 $\forall j,\Sigma_{i=1}^Na_{ij}\leq1$
订单分配的关键是估计每个司机接单的概率, 然后进一步就可以计算一个订单被司机接受的概率了,因此将订单分配模型划分为两部分:一个模型预测司机的行为,即预测每个司机接单的概率;另一个模型最大化目标函数 $E_{SR}$。
2. 司机行为预测模型
司机的行为有两种——接受订单和拒绝订单,并用变量 $y$ 来表示司机行为的结果,$y$ 是一个二值变量,接受为1,拒绝为0。假设司机的行为服从一个独立同分布。
用 $p_{ij}$ 表示订单 $o_i$ 被司机 $d_j$ 接受的概率,这个概率可能受到订单的价格、行驶距离和目的地方向等诸多因素的影响,这些因素可以编码为一个特征向量 $x_{ij}$。给定 $x_{ij}$,需要估计一个司机的接受概率,即:
$$
p_{ij}=p(y=1|x_{ij})
$$
这样就把司机行为的预测问题转变成了一个经典的二分类问题。
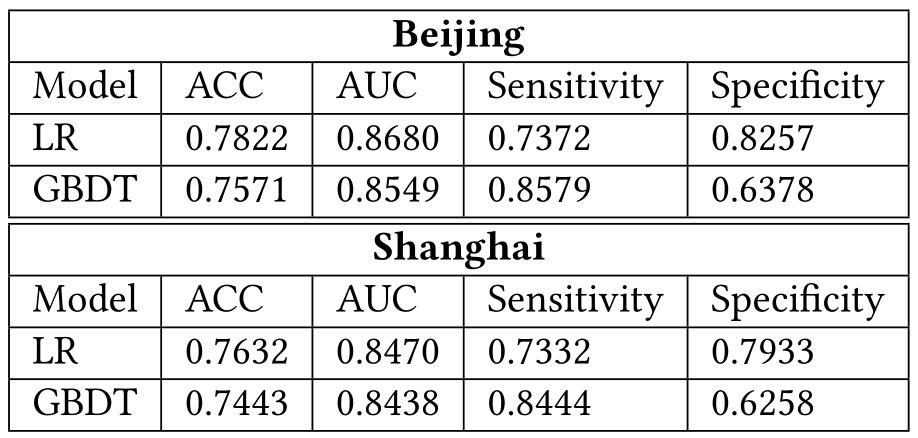
文章测试了 LR(logistic regression)和 GBDT(梯度提升决策树)在两个数据集上的 ACC(accuracy)和 AUC(曲线下面积),由上表可知,LR 模型的效果更好,所以最终选择 LR 模型最为司机行为预测模型,概率 $p_{ij}$ 可以写为:
$$
p_{ij}=p(y=1|o_i,d_j)=\frac{1}{\exp(-w^Tx_{ij})}
$$
司机行为预测模型主要考虑以下因素:
- 订单-司机相关特征:接车距离、订单目的地是否在司机的行驶方向的前方
- 订单相关特征:出发地和目的地之间的距离、预计到达时间(ETA)、目的地的类别(机场、旅馆、学校、工作场所等)、交通状况、目的地的历史订单频率
- 司机相关特征:司机的接单率、司机活动的范围、司机偏爱的订单距离
- 其他特征:是否是工作日、一天中的时刻、订单附件的司机数
假设 $N$ 个订单被分配给 $M$ 个司机,则订单 $o_i$ 被接受的概率为:
$$
E_i=1-\Pi^M_{j=1}(1-p_{ij})^{a_{ij}}
$$
所以,成功率 $E_{SR}$ 为:
$$
E_{S R}=\frac{\sum_{i=1}^{N}\left[1-\prod_{j=1}^{M}\left(1-p_{i j}\right)^{a_{i j}}\right]}{N}
$$
加上每个司机同时最多接受一个订单的约束条件,最终的订单分配问题可以表示为:
$$
\left{\begin{array}{c}
\max {a{i j}} E_{S R}=\frac{\sum_{i=1}^{N}\left[1-\prod_{j=1}^{M}\left(1-p_{i j}\right)^{a_{i j}}\right]}{N} \
\text { s.t. } \forall j, \sum_{i=1}^{N} a_{i j} \leq 1, a_{i j} \in{0,1}
\end{array}\right.
$$
很多组合优化问题都是 NP 难问题,通常没有通用的高效算法来解决,这里选用的是爬山法(hill-climbing method)来解决该问题,算法流程如下:

三、目的地预测
$$
\begin{array}{lll}
\hline \text { Symbol } & \text { Meaning } & \text { Range } \
\hline T & \text { time of day } & {[0,24)} \
D & \text { Day of the week } & \text { workday, holiday } \
\text {Lng} & \text { Departure Longi- } & {[-180,180]} \
& \text { tude } & \
\text {Lat} & \text { Departure } & {[-90,90]} \
& \text { Latitude } & \
Y & \text { Description } & \begin{array}{l}
\text { Set of User Historic Destina- } \
\text { tions, }\left{y_{1}, y_{2}, \ldots, y_{i}, \ldots, y_{n}\right}
\end{array} \
\hline
\end{array}
$$
同一个用户通常在相似的时间回去相同的目的地,同一个用户去的目的地集合基本是固定的,订单的位置对目的地预测很重要。
用贝叶斯公式来表达用户去目的地 ${y_1,y_2,…,y_i,…,y_n}$ 的条件概率:
$$
p\left(Y=y_{i} | X\right)=\frac{p\left(X | Y=y_{i}\right) p\left(Y=y_{i}\right)}{\sum_{j=1}^{n} p\left(X | Y=y_{j}\right) p\left(Y=y_{j}\right)}
$$
其中 $X=(T,Lng,Lat)$ 表示出发时间、出发经度和出发维度。可以通过用户的历史出行记录来估计 $p(Y=y_i)$:
$$
p\left(Y=y_{i}\right)=\frac{\operatorname{freq}\left(y_{i}\right)}{\sum_{j=1}^{n} \operatorname{freq}\left(y_{j}\right)}
$$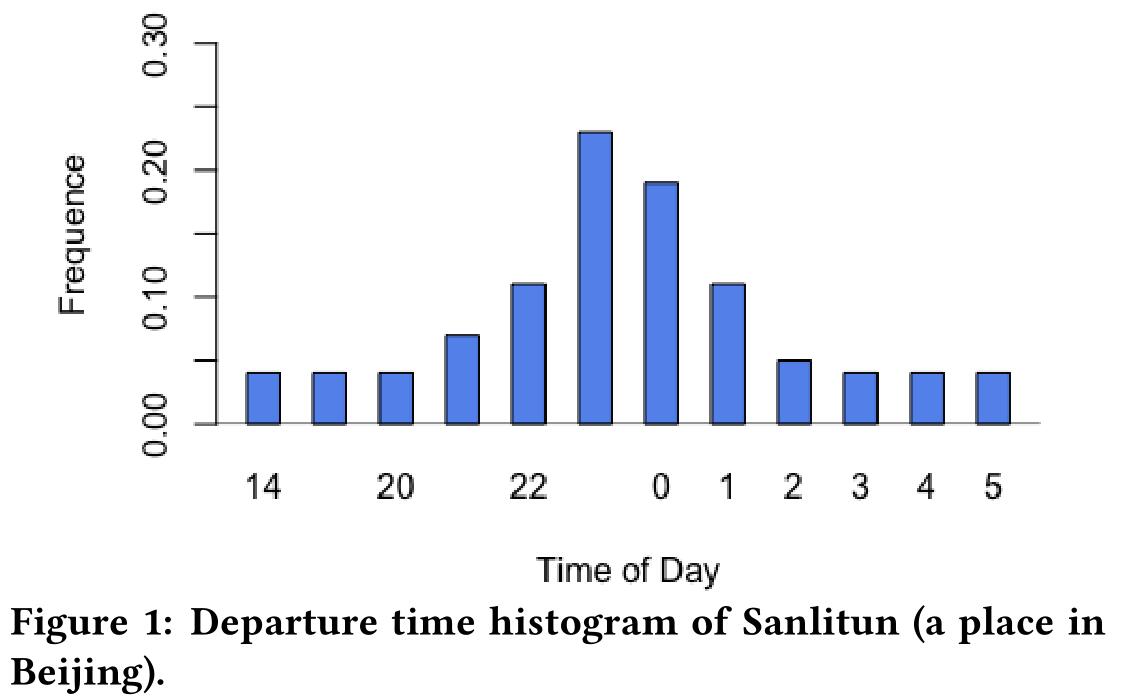
通过上图可知,用户在不同时间出行的目的地近似服从高斯分布,所以用高斯分布来估计关于出发时间 $T$ 的条件概率:
$$
T | Y=y_{i} \sim N\left(\mu_{i}, \sigma_{i}^{2}\right)
$$
并且可以发现变量 $T$ 是循环性的,它的值从0到23,然后重复。因此高斯分布的均值 $\mu_i$ 和方差 $\sigma_i^2$ 不能用传统的方法来估计,一个计算循环量均值的方法是先将所有的循环量转换为单位向量,然后计算向量的均值,并将结果转换为原始的循环表示。给定时间 $t_1,t_2,…,t_m$,均值可以通过下式计算:
$$
\mu=\frac{24}{2 \pi} \cdot \arctan \left[\frac{1}{m} \sum_{k=1}^{m} \sin \left(\frac{2 \pi}{24} \cdot t_{k}\right), \frac{1}{m} \sum_{k=1}^{m} \cos \left(\frac{2 \pi}{24} \cdot t_{k}\right)\right]
$$
但是通过该公式计算出的结果与真实结果会存在偏差,并且在某些特定情况(当sin和cos的求和项为0时)下,会无解。为了解决该问题,文章提出了一个计算出发时间均值和方差的方法。出发时间的均值可以通过求解以下二次优化问题来获得:
$$
\left{\begin{array}{l}
\min {\mu} \sum{k=1}^{m}\left[\operatorname{distance}\left(t_{k}, \mu\right)\right]^{2} \
\text { s.t. } \mu \in[0,24)
\end{array}\right. 公式()
$$
其中 $distance(t_1,t2)$ 表示两个循环变量 $t_1$ 和 $t_2$ 之间的距离,定义如下:
$$
\operatorname{distance}\left(t_{1}, t_{2}\right)=\left{\begin{array}{ll}
\left|t_{1}-t_{2}\right| & \text { if }\left|t_{1}-t_{2}\right| \leq 12 \
24-\left|t_{1}-t_{2}\right| & \text { if }\left|t_{1}-t_{2}\right|>12
\end{array}\right.
$$
也可以简写为:
$$
\operatorname{distance}\left(t_{1}, t_{2}\right)=-\left|\left(\left|t_{1}-t_{2}\right|-12\right)\right|+12
$$
将其带入公式() 中得:
$$
\left{\begin{array}{l}
\left.\min {\mu} \sum{k=1}^{m}\left[\left|\left(\left|t_{k}-\mu\right|-12\right)\right|-12\right)\right]^{2} \
\text { s.t. } \mu \in[0,24)
\end{array}\right.
$$
同理,可以通过类似的方法估计方差 $\sigma^2$:
$$
\sigma^{2}=\frac{1}{m-1} \sum_{k=1}^{m}\left[\left|\left(\left|t_{k}-\mu\right|-12\right)\right|-12\right]^{2}
$$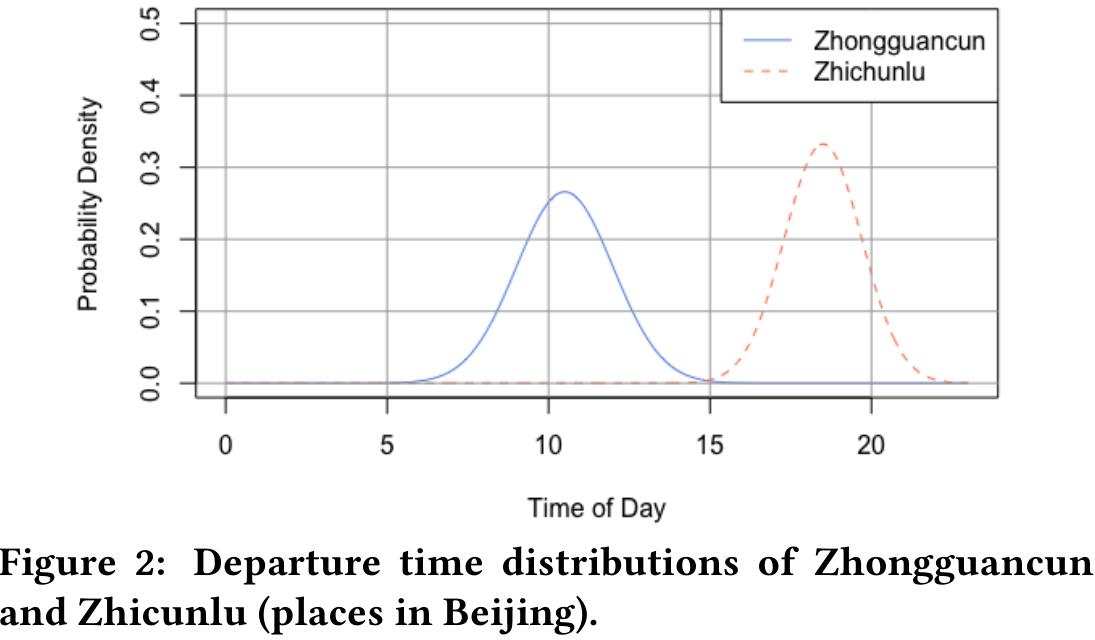
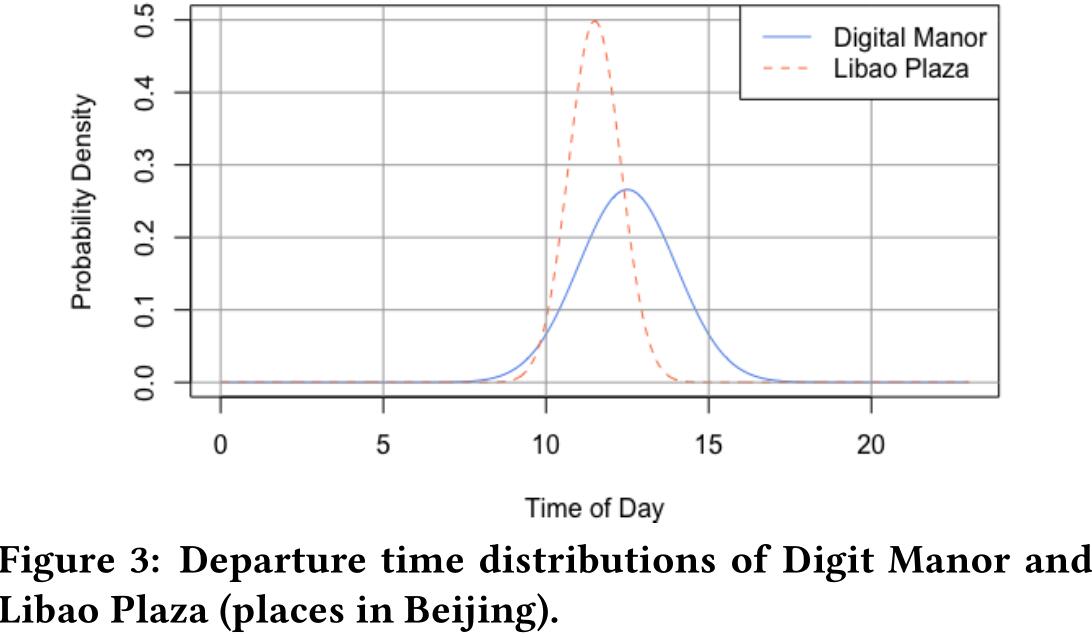
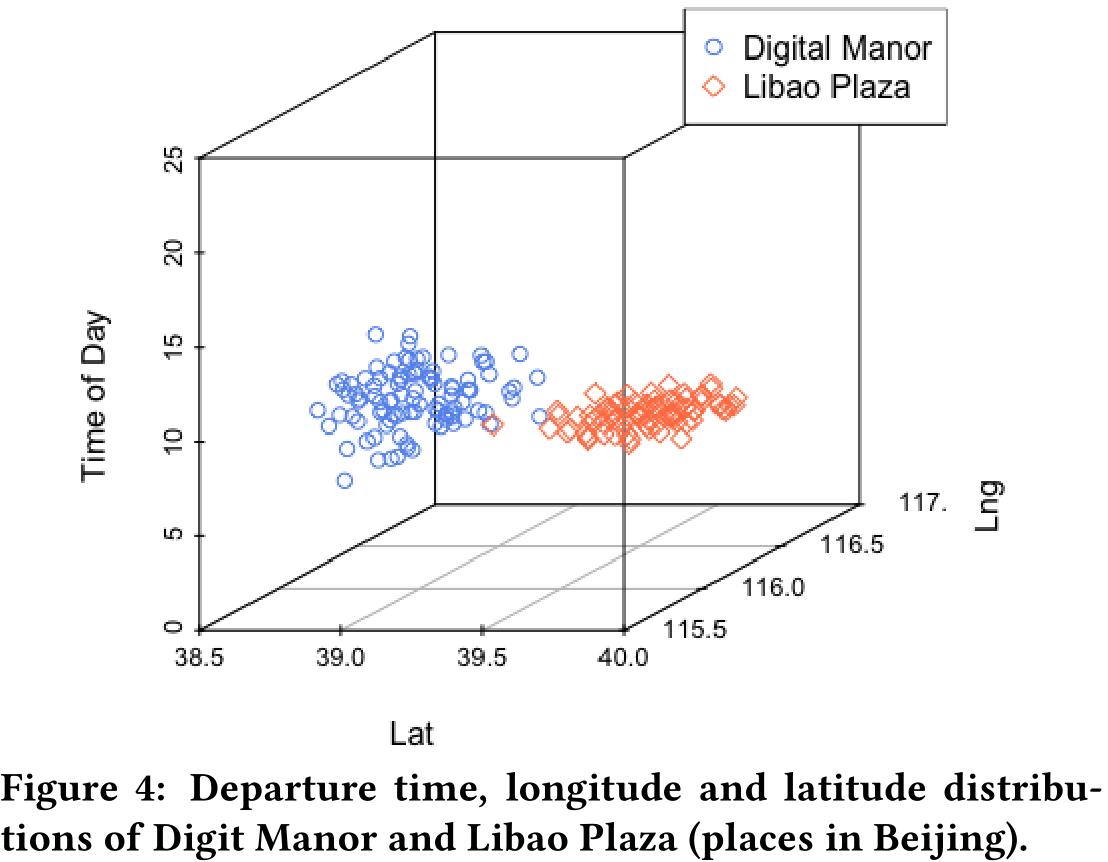
图二表示去中关村和知春路关于时间的分布,可以发现给定时间很容易区分目的地是哪;而图三表示去数字庄园和丽宝广场关于时间的分布,可以发现两者的重合比较严重,给定时间很难区分目的地是哪;图四表示去数字庄园和丽宝广场关于时间、经纬度的分布,在三维空间下给定时间、经纬度很容易区分目的地。通过以上三个图可以发现,三维分布能更容易的区分出两个不同的目的地。假设在给定目的地 $y_i$ 时,订单的经纬度和时间的条件概率满足三维高斯分布:
$$
\text { Lat, } \operatorname{Lng}, T | Y=y_{i} \sim N_{3}\left(\boldsymbol{\mu}{i}, \Sigma{i}\right)
$$
以下是目的地预测的完整过程:
估计每个用户目的地的均值 $\mu_i$ 和方差 $\sigma_i$
计算 $p(Y=y_i)$:
$$
p\left(Y=y_{i}\right)=\frac{\operatorname{freq}\left(y_{i}\right)}{\sum_{j=1}^{n} \operatorname{freq}\left(y_{j}\right)}
$$
并计算 $p(T,Lat,Lng|Y=y_i)$利用贝叶斯公式计算 $p(Y=y_i|T,Lat,Lng)$:
$$
\begin{array}{c}
p\left(Y=y_{i} | T, L a t, \ln g\right)= \
\frac{p\left(T, \operatorname{Lat}, \operatorname{Lng} | Y=y_{i}\right) p\left(Y=y_{i}\right)}
{\sum_{j=1}^{n} p\left(T, \operatorname{Lat}, \operatorname{lng} | Y=y_{j}\right) p\left(Y=y_{j}\right)}
\end{array}
$$按照概率 $p(Y=y_i|T,Lat,Lng)$ 对目的地进行排序,并给出一个列表
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/05/18/TODM/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


