【论文笔记】基于DQN和知识迁移的订单分配模型

2020-05-18

本文是论文《Deep Reinforcement Learning with Knowledge Transfer for Online Rides Order Dispatching》的阅读笔记。

一、介绍

文章把订单分配问题建模成一个 MDP，并且提出了基于 DQN 的解决策略，为了增强的模型的适应性和效率，文章还提出了一种相关特征渐进迁移（Correlated Feature Progressive Transfer）的方法，并证明了先从源城市学习到分配策略，然后再将其迁移到目标城市或者同一个城市的不同时间的方法，比没有迁移的学习效果要好。

订单分配问题有两个挑战，第一个挑战是提升订单分配的效率，另一个挑战是模型的可拓展性。之前的模型通常通过按照城市来将订单分配问题分解为小问题，将订单分配问题建模成一个 MDP，并通过离散的基于表格的方法进行求解，但是为每个城市构建一个模型并进行训练也是不太现实的。这种方法存在三个问题：

存在很多实时变化的因素，诸如交通的供需情况，这对于基于表格的方法来说是很难实时的考虑并处理的；
不同城市的出行过程被看作是具有相同结构的不同 MDP，而基于表格的方法不能实现在不同城市之间的知识迁移；
训练的收敛往往需要很长的时间。

由于强化学习的方法在训练初期通常学习速度很慢，所以利用相关的先验知识进行迁移极大的提升了学习的效率。

二、MDP

智能体是从司机的角度来定义的，智能体主动去寻找适合当前司机的订单。一次出行包括接车和把乘客送到目的地两部分，然后司机就可以获得即时奖励，当然司机也可能是空闲的，此时收益为0。

状态 $s$：包括司机的地理位置和当前的时间（单位是秒），用 $s:=(l,t)$ 表示，其中 $l$ 是司机的经纬度，$t$ 是当前时间。除此之外，状态还可能包括一些额外的信息 $f$，如供需状态、附件订单的完成情况等，此时状态表示为 $s:=(l,t,f)$。

动作 $a$：将订单分配给一个司机，用 $s_0:=(l_0,t_0,f_0)$ 表示当前的状态，用 $s_1:=(l_1,t_1,f_1)$ 表示到达目的地后的状态，那么行为可以表示为 $a=(l_1,t_1)$，所有的行为空间表示为 $\mathcal{A}$。

收益 $r$：一趟旅程的总收入，是关于状态和动作的函数。

episode：把一天看作一个 episode。

状态-行为值函数 $Q(s,a)$：是一个 episode 内司机的累计收益的期望，表示为 $Q(s, a):=E\left[\sum_{t=0}^{T} \gamma^{t} R\left(S_{t}, A_{t}\right) | S_{0}=s, A_{0}=a\right]$，$S,A,R$ 是 $s,a,r$ 的随机变量。$T$ 是到达终点状态经过的步数，把时间划分为10分钟为一步。

策略 $\pi(a|s)$：是从状态到行为的一个映射，关于 $Q(s,a)$ 的贪心策略表示为 $\pi(s):=\arg \max _{a} Q(s, a)$

状态值函数 $V(s)$：从某个状态 $s$ 开始，按照策略 $\pi$ 采取行动，一个 episode 内司机所得到的累计收益的期望。当采取关于 $Q(s,a)$ 的贪心策略时，状态值函数为 $V(s):=Q(s,\pi(s))=\max_{a\in\mathcal{A}}Q(s,a)$

三、带有行为搜索的 DQN

1. 模型

为了提升训练的稳定性，使用了 Double-DQN，并使用用户的历史出行数据来进行训练，同时简单的合成了一些数据用作数据增强。

2. 行为搜索

通过构造行为的近似可行空间 $\hat{\mathcal{A}}(s)$ 来近似求解 $Q(s,a)$，文章不是在所有的有效动作中进行搜索，而是从 $s$ 附近的历史行程中搜索
$$
\tilde{\mathcal{A}}(s):=\left{x_{s_{1}} | x \in \mathcal{X}, B\left(x_{s_{0}}\right)=B(s)\right}
$$
其中 $\mathcal{X}$ 是所有行程的集合，$B(s)$ 是 $s$ 所属的离散的时空，文章将地区划分成多个六边形仓，每个六边形仓由其中心点坐标表示，搜索空间越大，需要的计算时间就越长，所以文章把搜索时的行为数设成一个可训练的参数。在策略估计时，也是用类似的搜索过程，那时会利用历史出行数据来模拟司机一天的轨迹。

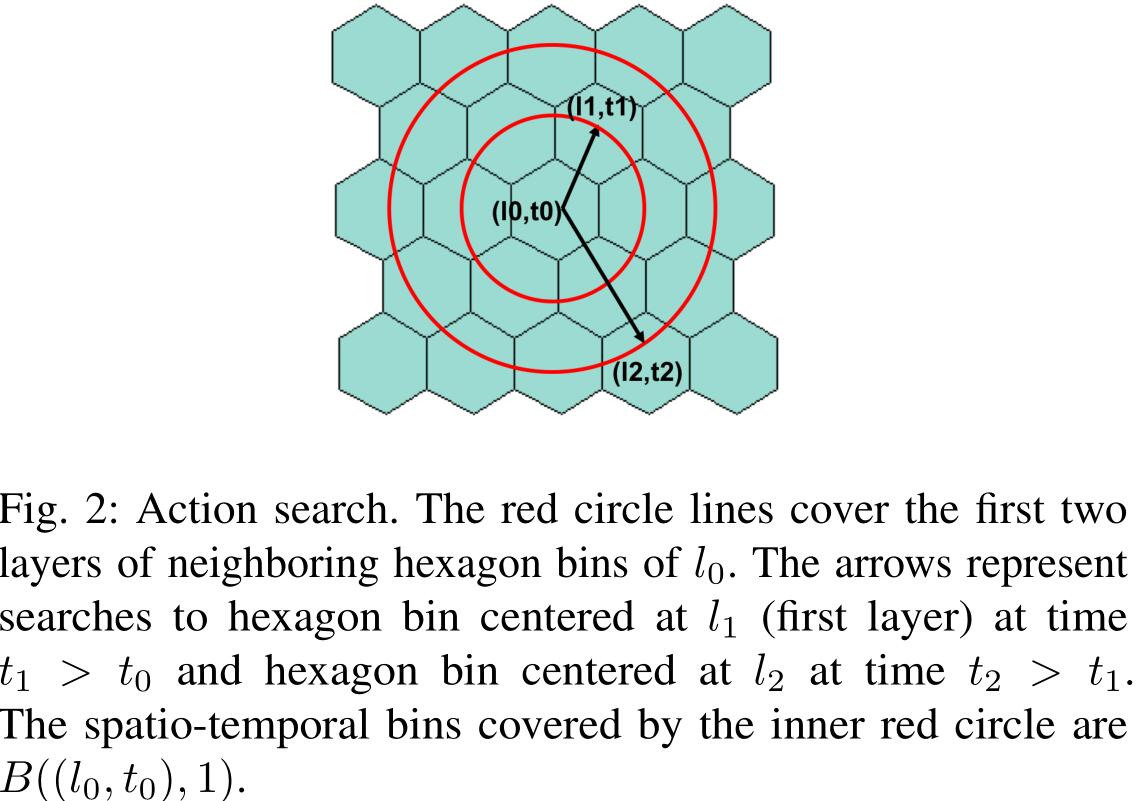
行为搜索的伪代码如下：

3. 拓展行为搜索

在早上时在一个偏远地区进行搜索可能会返回一个空集，这时就需要在时间和空间上进行拓展动作搜索。第一种搜索方向是保持下车的位置不变，等待下一轮进行搜索，直到以下情况的一种发生：

如果 $\hat{\mathcal{A}}(s’)$ 非空，则返回 $\hat{\mathcal{A}}(s’)$
如果到达终止状态，则返回终止状态
如果 $s’_t$ 超过了等待时间的上限，则返回 $s’$

第二种搜索方向是通过分层的方式对当前位置的相邻六边形进行拓展搜索，定义 $L$ 层的时空仓为 $B(s,L)$，源自该时空仓的历史出行数据的集合为：
$$
\tilde{\mathcal{A}}(s, L):=\left{x_{s_{1}} | x \in \mathcal{X}, B\left(x_{s_{0}}\right) \in B(s, L)\right}
$$
当 $\tilde{\mathcal{A}}(s, L)$ 非空时，则停止增加 $L$，并返回 $\tilde{\mathcal{A}}(s, L)$；反之返回 $B(s,L_{max})$，即六边形仓的中心点及其相应的时间。$L_{max}$ 是用来控制搜索空间的最大层数。

4. 终止状态值

当一个 episode 结束时，无论位置如何， $Q(s,a)$ 的值应该接近于0，在每次训练的开始，将 $s_1$ 作为终止状态放入回放池中，这样可以加快收敛。

5. 在多司机匹配环境下的配置

我们将调度窗口中收集的订单分配给一组司机，以最大化分配的总价值。
$$
\arg \max {a \in \mathcal{A}^{\prime}} \sum{s \in \mathcal{S}} Q(s, a(s))
$$
其中 $a(s)$ 是从多个订单中选择一个订单分配给司机 $s$ 的分配函数，$\mathcal{A}’$ 是所有分配方程的空间，$S$ 是空闲司机的集合，订单和司机的匹配可以看作是二分图匹配问题，可以用 KM 算法来解决。

6. 表格形式中的状态值

$Q(s,a)$ 可以用 $r+V(B(s’))$ 来采样近似，$A:=r+V(B(s’))-V(B(s))$ is the advantage associated with the trip assignment x and is used as the edge weights.

$V^{}(B(s)):=\max _{a \in \tilde{\mathcal{A}}} Q^{}(s, a)$

$V^{\pi}(B(s)):=\operatorname{mean}_{a \in \tilde{\mathcal{A}}} Q^{\pi}(s, a)$

四、多城市迁移

考虑三种迁移学习的方法：微调、渐进网络（progressive network）和相关特征渐进迁移（CFPT），迁移学习共同的思想是利用从源城市学习到的参数应用的目标城市。

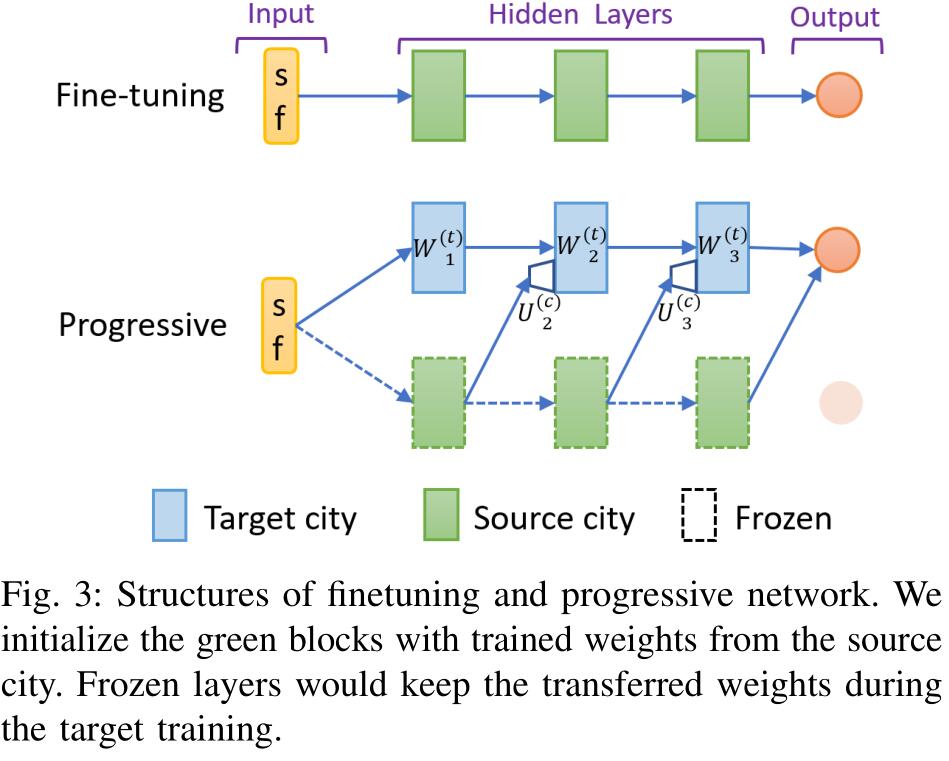
微调：先在源城市训练网络，然后再将训练得到的网络权重在目标城市网络中使用，参数在反向传播时微调。
渐进网络：通过与目标网络的横向连接利用训练权重，连接函数为：
$$
h_{i}^{(t)}=f\left(W_{i}^{(t)} h_{i-1}^{(t)}+U_{i}^{(c)} h_{i-1}^{(s)}\right)
$$
其中 $W_i^{(t)}$ 表示目标网络第 $i$ 层的权重矩阵，$U_i^{(c)}$ 表示来自源任务网络的横向连接权重矩阵，$h_i^{(t)}$ 和 $h_i^{(s)}$ 表示目标网络和源网络第 $i$ 层的输出。$f(\cdot)$ 是激活函数。

如图三中 Progressive 图所示，首先训练一个源网络（绿色），然后将其乘以横向连接权重连接到目标网络（蓝色），在目标网络的训练过程中源网络（绿色）的权重保持不变。
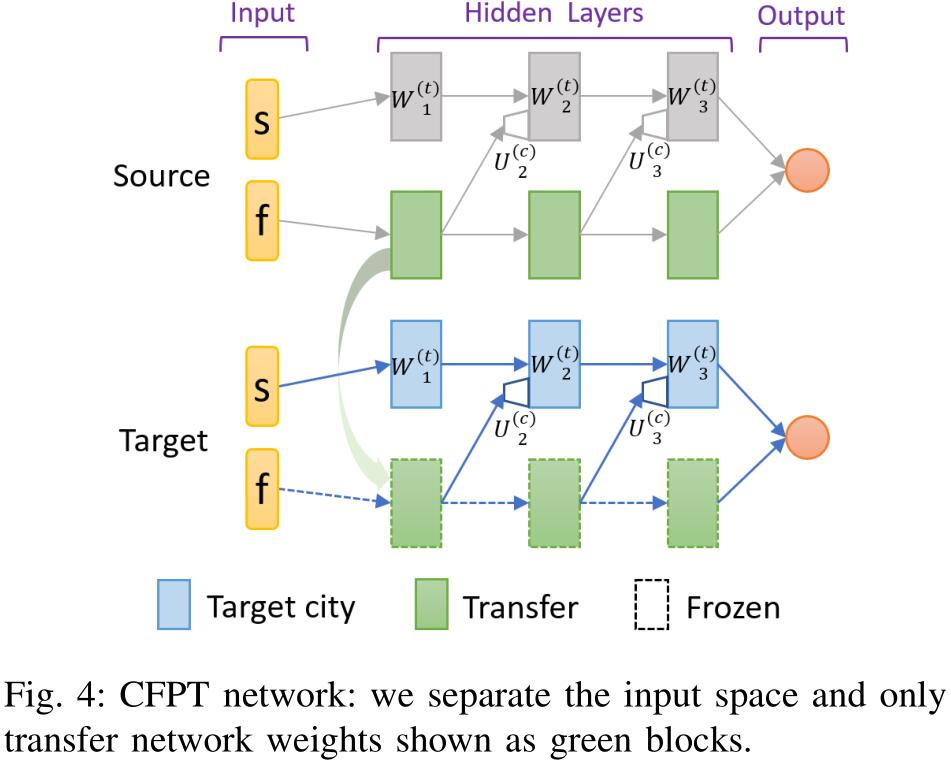
CFPT：由于状态空间是十分多样的，所以并不是所有的状态元素对于不同的城市都适应。按照图四为源城市训练一个平行的渐进结构，其连接函数和横向连接中用到的相同。网络的输入也分成了两部分：$s$ 表示那些直觉上不适应目标城市的元素，$f$ 表示那些适应目标城市的元素。目标网络和源网络结构相同，并且重用源网络中渐进部分（图四中绿色的块）的权重。CFPT 的创新性在于当训练源网络时，把网络分成了两个平行流，下面的流只关心输入 $f$。我们将相关特征输入 $f$ 看作是时空位移向量和实时上下文特征之间的连接，三元时空位移向量通过 $(s_1-s_0)$ 计算得到，

五、实验
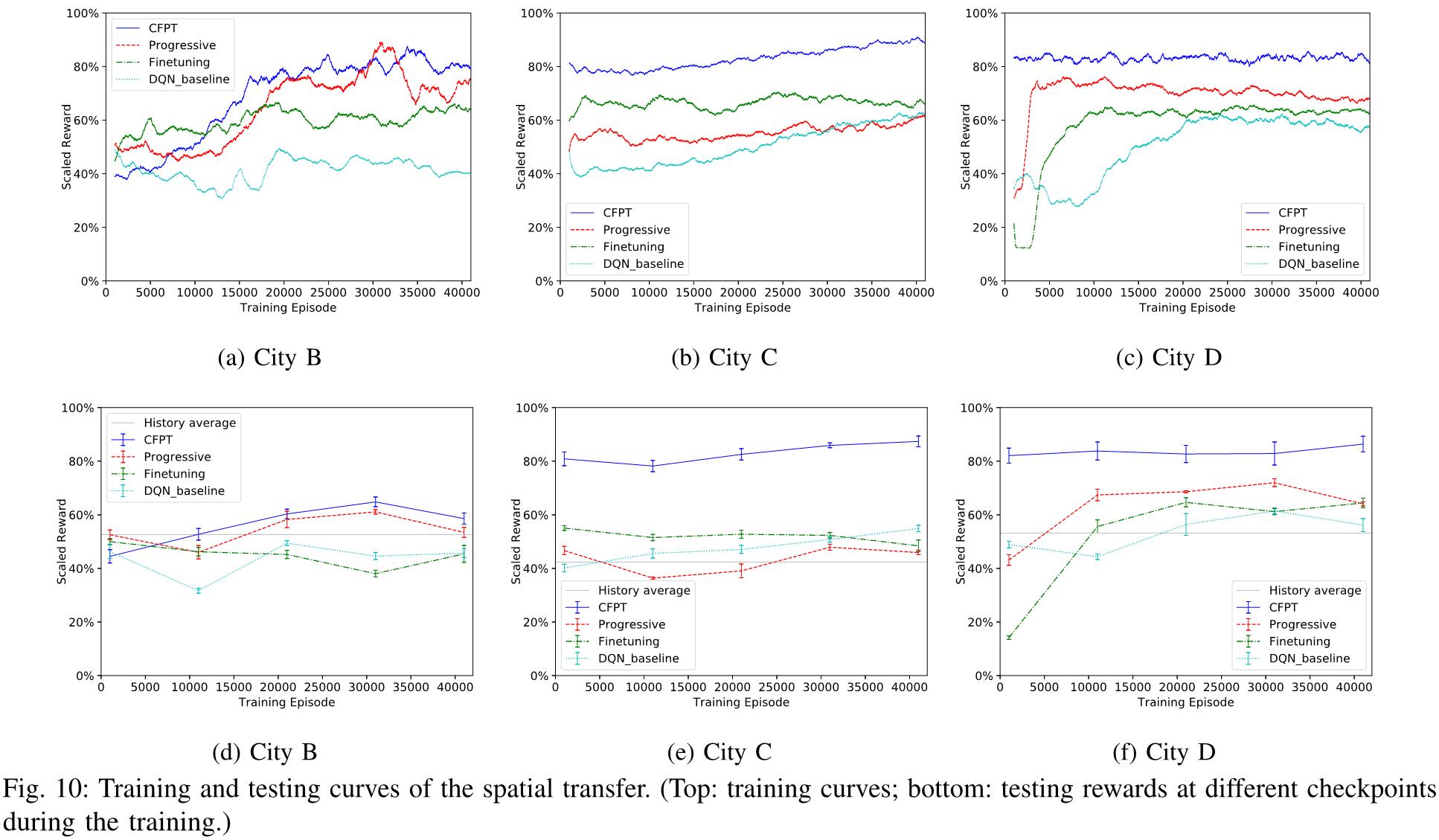
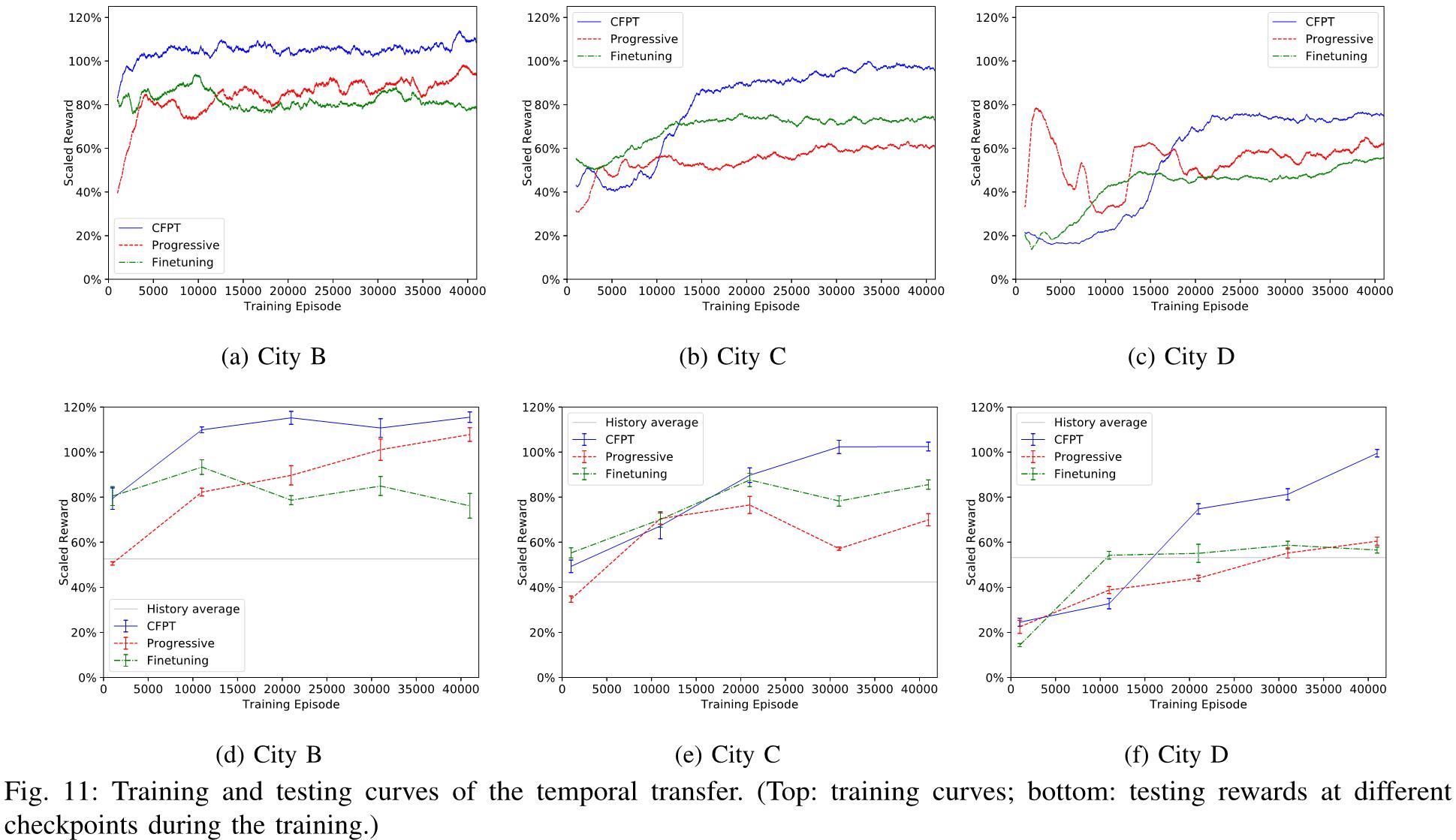
为了实现对目标城市的鲁棒有效的网络训练，文章进行了两种类型的迁移实验，包括空间迁移和时间迁移。在空间迁移方面，将 A 市作为源城市，将其他三个城市作为目标城市。对于时间迁移，以一个月数据训练的城市模型为源，以一个月后数据训练的同一城市模型为目标。