本文是关于论文《Probabilistic Multilayer Regularization Network for Unsupervised 3D Brain Image Registration》的阅读笔记。
文章提出了一个无监督的3D脑部图像配准网络,用来捕获 fixed image 和 moving image 之间特征级(feature-level)的信息。网络包括分别对 fixed image 和 moving image 进行处理的两个深度CNN,以及一个对以上两个CNN处理结果进行对齐的特征级概率网络。这两种网络实现了不同级别的特征提取。
传统的基于模型(深度学习)的配准网络都忽视了两张输入图像之间的特征级的转换关系,CNN的隐藏层学习到的特征对于隐含变量(latent variable)来说是透明的,所以在本文中首先使用了两个CNN,一个CNN用来 fixed image 中提取特征,另一个从 moving image 中提取特征。此外,还用一个概率网络在两个CNN对应的隐藏层之间捕获它们的转换关系。此外还在CNN的多个层中嵌入了正则项,以在不同层产生特征级的隐含变量。最后,通过把在所有层中预测得到的特正级隐含变量结合,得到最终的用于配准的隐含变量。
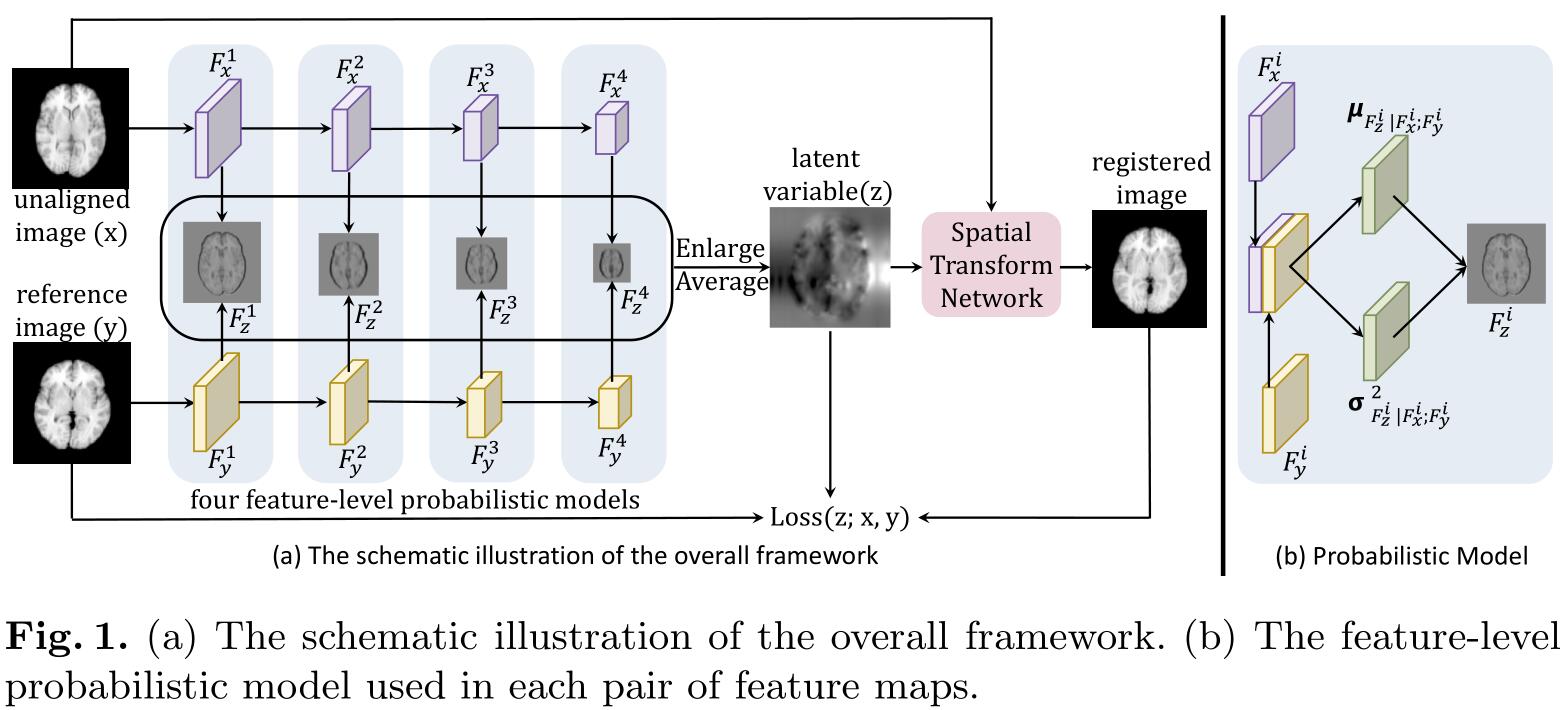
首先使用两个CNN产生两组具有不同分辨率的特征图集合,然后用一个特征级的概率推断模型来估计特征级的隐含变量,该隐含变量表示的是在两个CNN相同层的特征图之间的转换关系。然后把每一层产生的特征图扩大到相同的大小,将它们加起来产生最终的隐含变量 $z$。然后把 moving image $x$ 和隐含变量 $z$ 输入到空间转换网络(STN)中产生最终的配准后的图像。
$(F_x^i,F_y^i)$ 表示两个CNN第 $i$ 层产生的特征图,$F_z^i$ 表示概率模型产生的第 $i$ 层的隐含变量, 它实际是让 $F_x^i$ 对齐到 $F_y^i$ 的 STN 的参数,或者说形变场。在已知 $F_x^i,F_y^i$ 的情况下,可以通过最大化后验概率 $p(F_z^i|F_x^i;F_y^i)$ 来得到最优的 $F_z^i$。具体的,引入了一个近似后验概率 $q_\psi(F_z^i|F_x^i;F_y^i)$ ,然后最小化 $p(F_z^i|F_x^i;F_y^i)$ 和 $q_\psi(F_z^i|F_x^i;F_y^i)$ 之间的KL散度来使得两个分布尽可能的相似,该过程可以用下式表示:
$$
\begin{aligned}
& \min {\psi} K L\left[q{\psi}\left(F_{z}^{i} | F_{x}^{i} ; F_{y}^{i}\right) | p\left(F_{z}^{i} | F_{x}^{i} ; F_{y}^{i}\right)\right] \
=& \min {\psi} K L\left[q{\psi}\left(F_{z}^{i} | F_{x}^{i} ; F_{y}^{i}\right) | p\left(F_{z}^{i}\right)\right]-E_{q} \log p\left(F_{y}^{i} | F_{z}^{i} ; F_{x}^{i}\right)
\end{aligned}
$$
其中 $q_\psi(F_z^i|F_x^i;F_y^i)$ 来自于多元正态分布:
$$
q_{\psi}\left(F_{z}^{i} | F_{x}^{i} ; F_{y}^{i}\right)=\mathcal{N}\left(z ; \mu_{F_{z}^{i} | F_{x}^{i} ; F_{y}^{i}}, \sigma_{F_{z}^{i} | F_{x}^{i}, F_{y}^{i}}^{2}\right)
$$
其中 $\mu_{F_{z}^{i} | F_{x}^{i} ; F_{y}^{i}}$ 是分布的均值,$\sigma_{F_{z}^{i} | F_{x}^{i}, F_{y}^{i}}^{2}$ 是分布的方差,它们是通过概率模型得到的(如图1(b))。
$p(F_z^i)$ 和 $p(F_z^i|F_x^i;F_y^i)$ 符合以下多元正态分布:
$$
p\left(F_{z}^{i}\right)=\mathcal{N}\left(F_{z}^{i} ; 0, \sigma_{F_{z}^{i}}^{2}\right)
$$
$$
p\left(F_{y}^{i} | F_{z}^{i} ; F_{x}^{i}\right)=\mathcal{N}\left(F_{y}^{i} ; F_{x}^{i} \circ \phi_{F_{z}^{i}}, \sigma_{F^{i}}^{2}\right)
$$
其中 $\sigma_{F_z^i}^2$ 是分布的方差, $F_{x}^{i} \circ \phi_{F_{z}^{i}}$ 是噪音,$\sigma_{F^i}^2$ 是噪音项的方差。

在CNN浅层的特征图具有较高的分辨率并且具有丰富的细节信息,而CNN深层的特征图具有较低的分辨率并且具有高层次的语义信息。高层语义信息可以帮助全局配准,但是忽略了很多细节。而细节信息则是捕获了局部的配准信息。所以将浅层到深层的特征图 $F_z^i$ 混合得到最终的隐含变量 $z$,然后输入到 STN 中,对 moving image 进行变形。
模型总的损失为:
$$
\mathcal{D}{\text {total}}=\mathcal{L}(z ; x, y)+\sum{i=1}^n w_{i} \mathcal{L}\left(F_{z}^{i} ; F_{x}^{i}, F_{y}^{i}\right)
$$
其中,$\mathcal{L}(z;x,y)$ 表示从输入图像 $x$ 和 $y$ 到输出的配准后的图像 $z$ 的KL散度,$\mathcal{L}\left(F_{z}^{i} ; F_{x}^{i}, F_{y}^{i}\right)$ 是从输入特征图 $F_x^i$ 和 $F_y^i$ 到输出配准转换变量 $F_z^i$ 的KL散度。$n$ 是CNN的层数,$w_i$ 是第 $i$ 层损失的权重。通常设置$n=4,w_i=1$。基于KL散度的损失为:
$$
\mathcal{L}(Z ; X, Y)=\frac{1}{2 \sigma_{Z | X ; Y}^{2}}\left|Y-X \circ \phi_{Z}\right|^{2}+\frac{1}{2}\left[\operatorname{tr}\left(\sigma_{Z | X ; Y}^{2}\right)+\left|\mu_{Z | X ; Y}\right|-\log \operatorname{det}\left(\sigma_{Z | X ; Y}^{2}\right)\right]
$$
其中第一项是使得配准后的图像 $X\circ\phi_Z$ 与图像 $Y$ 相似的重建损失,第二项是公式1第一项的近似,它可以让 $q_\psi(Z|X;Y)$ 与 $p(Z)$ 相似;$\mu_{Z|X;Y}$ 和 $\sigma_{Z|X;Y}$ 分别是分布 $q_\psi(Z|X;Y)$ 的均值和标准差。
初始学习率为 $1e^{-4}$,并且周期性的减少(乘以0.1),一共有100个epoch,使用Adam优化器,优化器的第一个动量为0.9,第二个动量为0.999,衰减权重为0.0001。
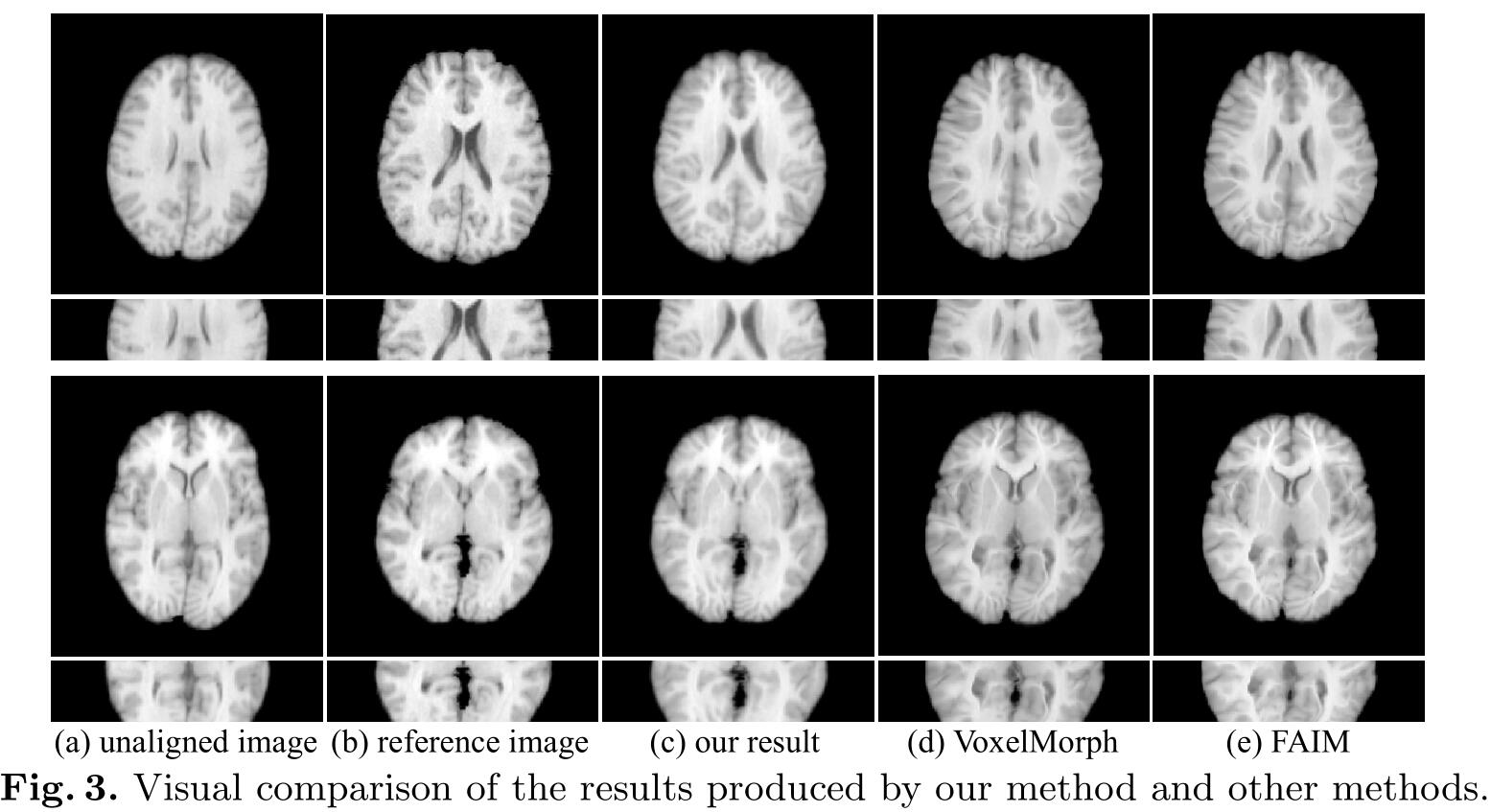
下图是实验的结果对比图。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/05/11/PMRN/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


