本文是论文《DeepAtlas: Joint Semi-Supervised Learning of Image Registration and Segmentation》的阅读笔记。
文章第一个提出了一个图像配准和图像分割联合学习的网络模型 DeepAtlas,该模型实现了弱监督的图像配准和半监督的图像分割。在图像配准时使用图像的分割标签作为监督数据,如果没有分割标签,则通过分割网络产生;而经过配准后的图像增加了在图像分割时可利用的训练数据的量,相当于是一种数据增强。该模型不仅在分割和配准的精度上有所提升,并且还可以在训练数据有限的情况下实现较好的效果。
一、记号
- $I_m$:浮动图像(moving image)
- $I_t$:目标图像(target image)
- $\mathcal{F}_R$:配准网络
- $\theta_r$:配准网络的参数
- $\mathcal{F}_S$:分割网络
- $\theta_s$:分割网络的参数
- $u=\mathcal{F}_R(I_m,I_t;\theta_r)$:形变场
- $\phi^{-1}=u+id$:形变图,其中 $id$ 是恒等变换
- $I_m^w=I_m\circ\phi^{-1}$:配准后的图像
- $S_t$:目标图像分割标签
- $S_m^w=S_m\circ\phi^{-1}$:配准后图像分割标签
二、网络结构
DeepAtlas 的目的是当数据集中只有少量的分割标签可用时,通过联合训练来让分割和配准实现较高的精度。
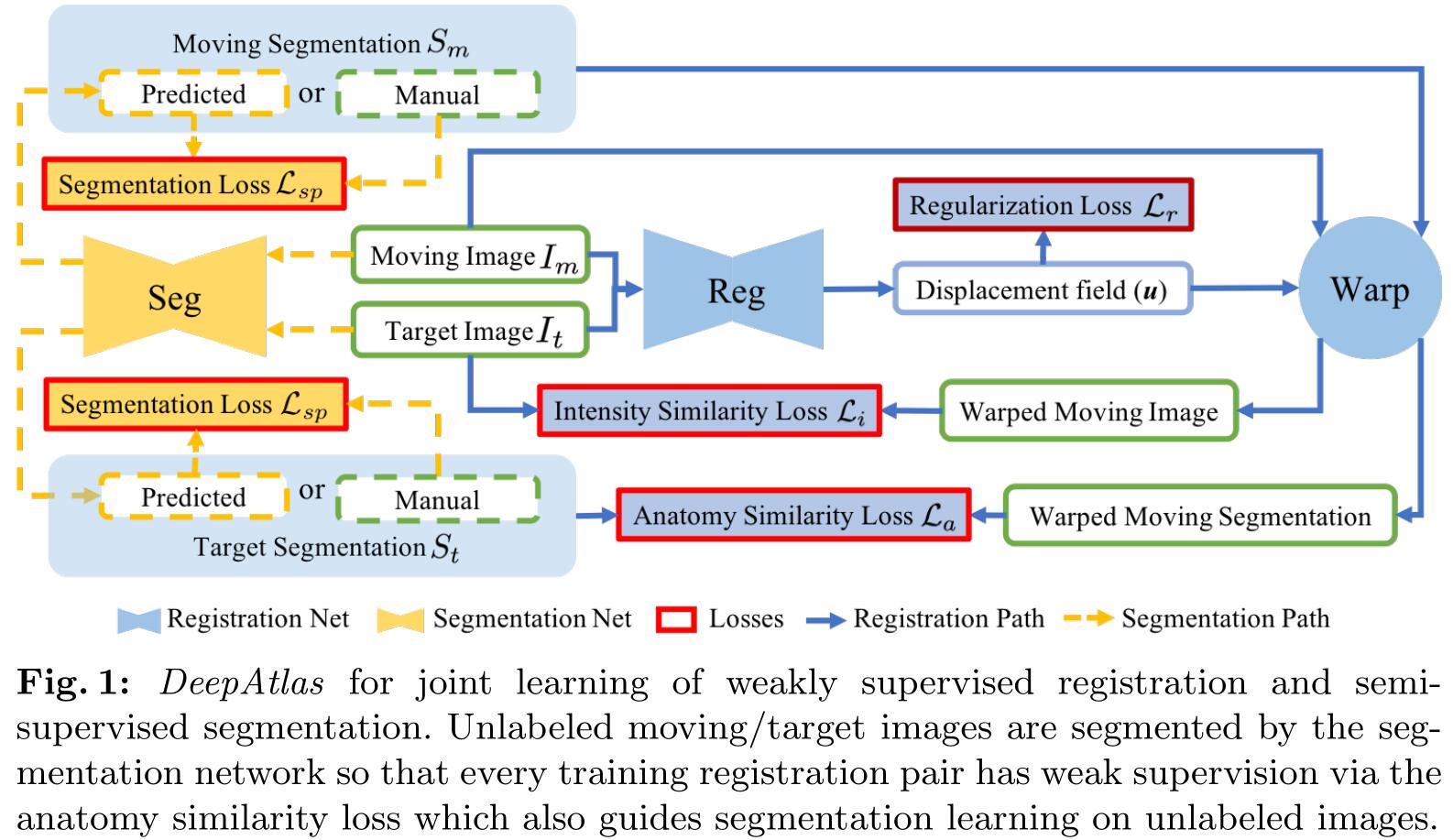
网络的结构如上图所示,蓝色的实线表示弱监督的配准,黄色虚线表示半监督的分割。
文章在附件中给出了分割网络和配准网络的具体结构,如下图左右两图所示:
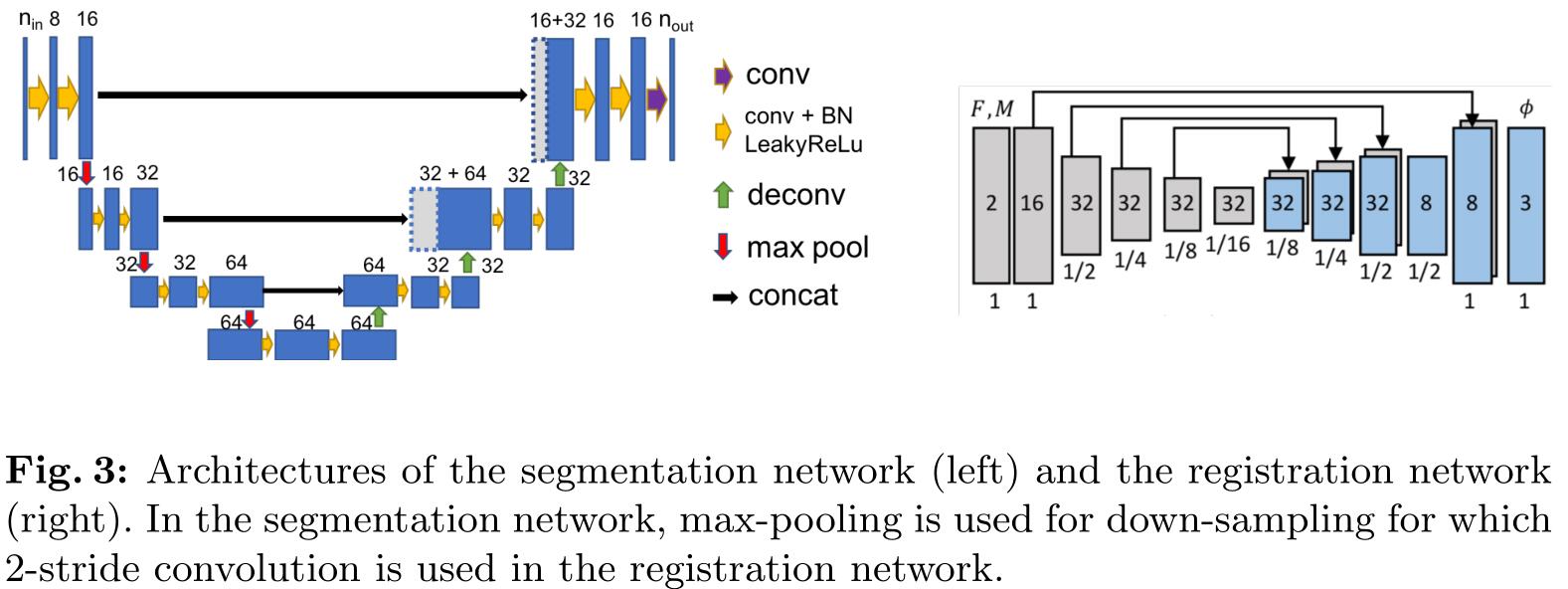
1. 配准网络
配准网络的损失主要有三个损失函数组成:配准正则损失 $\mathcal{L}_r$,图像相似度损失 $\mathcal{L}_i$ 和解剖损失(分割相似度损失) $\mathcal{L}_a$。配准正则损失 $\mathcal{L}_r$ 可以让形变场 $\phi$ 变得光滑,图像相似度损失 $\mathcal{L}_i$ 用来评价浮动图像 $I_m$ 和配准后图像 $I_m^w$ 之间的相似度,解剖损失(分割相似度损失) $\mathcal{L}_a$ 是目标图像分割标签 $S_t$ 和配准后图像分割标签 $S_m^w$ 之间的相似度损失。
如此一来,配准学习的过程可以由下式表示:
$$
\theta_{r}^{\star}=\underset{\theta_{r}}{\operatorname{argmin}}\left{\mathcal{L}{i}\left(I{m} \circ \Phi^{-1}, I_{t}\right)+\lambda_{r} \mathcal{L}{r}\left(\Phi^{-1}\right)+\lambda{a} \mathcal{L}{a}\left(S{m} \circ \Phi^{-1}, S_{t}\right)\right}
$$
其中 $\lambda_r,\lambda_a\geq0$。
2. 分割网络
分割网络的输入是一张图像 $I$,输出相应的分割结果 $\hat{S}=\mathcal{F}S(I;\theta_s)$,分割网络的损失主要有两个损失函数组成:解剖损失 $\mathcal{L}_a$ 和有监督分割损失 $\mathcal{L}{sp}$。解剖损失和配准网络中的相同,有监督的分割损失 $\mathcal{L}{sp}(\hat{S},S)$ 是分割网络的分割结果 $\hat{S}$ 和人工分割结果 $S$ 之间的相似度损失。但是浮动图像 $I_m$ 和目标图像 $I_t$ 的分割标签的存在情况有多种可能,所以相应的损失函数也存在以下四种情况:
$$
\left{\begin{array}{l}
\mathcal{L}{a}=\mathcal{L}{a}\left(S{m} \circ \Phi^{-1}, \mathcal{F}{\mathcal{S}}\left(I{t}\right)\right) \text { and } \mathcal{L}{s p}=\mathcal{L}{s p}\left(\mathcal{F}{\mathcal{S}}\left(I{m}\right), S_{m}\right), \text { if } I_{t} \text { is unlabeled; } \
\mathcal{L}{a}=\mathcal{L}{a}\left(\mathcal{F}{\mathcal{S}}\left(I{m}\right) \circ \Phi^{-1}, S_{t}\right) \text { and } \mathcal{L}{s p}=\mathcal{L}{s p}\left(\mathcal{F}{\mathcal{S}}\left(I{t}\right), S_{t}\right), \text { if } I_{m} \text { is unlabeled; } \
\mathcal{L}{a}=\mathcal{L}{a}\left(S_{m} \circ \Phi^{-1}, S_{t}\right) \text { and } \mathcal{L}{s p}=\mathcal{L}{s p}\left(\mathcal{F}{\mathcal{S}}\left(I{m}\right), S_{m}\right), \text { if } I_{m} \text { and } I_{t} \text { are labeled; } \
\mathcal{L}{a}=\mathcal{L}{s p}=0, \text { if both } I_{t} \text { and } I_{m} \text { are unlabeled. }
\end{array}\right.
$$
分割的学习过程可以由下式表示:
$$
\theta_{s}^{\star}=\underset{\theta_{s}}{\operatorname{argmin}}\left(\lambda_{a} \mathcal{L}{a}+\lambda{s p} \mathcal{L}{s p}\right), \quad \lambda{a}, \lambda_{s p} \geq 0
$$
三、实施细节
- 解剖相似度损失 $\mathcal{L}{a}$ 和有监督的分割损失 $\mathcal{L}{sp}$ 采用的是 soft multi-class Dice loss:
$$
\mathcal{L}{\text {dice}}\left(S, S^{\star}\right)=1-\frac{1}{K} \sum{k=1}^{K} \frac{\sum_{x} S_{k}(x) S_{k}^{\star}(x)}{\sum_{x} S_{k}(x)+\sum_{x} S_{k}^{\star}(x)}
$$
其中 $k$ 表示分割标签的下标,$x$ 是体素位置,$S$ 和 $S^*$ 是两个要比较的分割标签。
- 图像相似度损失 $\mathcal{L}_i$ 采用的是正则化的互相关(NCC):
$$
\mathcal{L}{i}\left(I{m}^{w}, I_{t}\right)=1-N C C\left(I_{m}^{w}, I_{t}\right)
$$
- 配准正则损失 $\mathcal{L}_r$ 采用的是弯曲能(bending energy):
$$
\mathcal{L}{r}(\mathbf{u})=\frac{1}{N} \sum{\mathbf{x}} \sum_{i=1}^{d}\left|H\left(u_{i}(\mathbf{x})\right)\right|_{F}^{2}
$$
其中 $||\cdot||_F$ 表示弗罗贝尼乌斯范数(Frobenius norm),$H(u_i(x))$ 是第 $i$ 个成分 $u(x)$ 的 Hessian 矩阵,$d$ 表示维度,$N$ 表示体素数。
在训练时,会交替的训练分割网络和配准网络,当一个网络在训练时,另一个网络的参数保持不变,并且是每训练配准网络20次才训练分割网络1次,这是因为分割网络更容易收敛。
四、实验结果
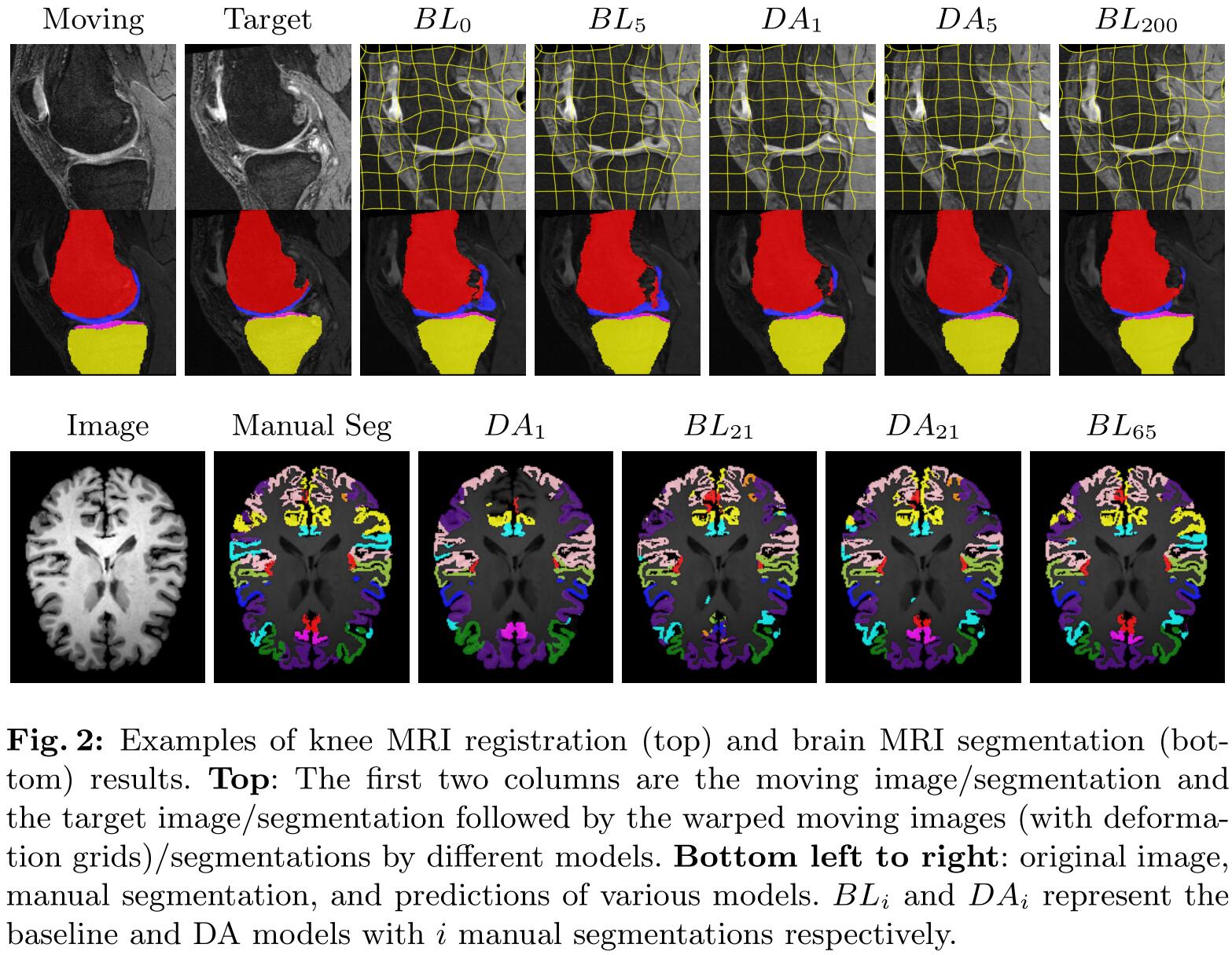
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/05/11/DeepAtlas/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


