本文是转载的文章:WGAN-GP(改进的WGAN)介绍。
WGAN是一篇好文章,但是在处理Lipschitz条件时直接把weight限制住也带来了一些问题,很快改进版的WGAN-GP便问世了,本文将带着大家一起看看 WGAN-GP的原理。
WGAN-GP是针对WGAN的存在的问题提出来的,WGAN在真实的实验过程中依旧存在着训练困难、收敛速度慢的 问题,相比较传统GAN在实验上提升不是很明显。WGAN-GP在文章中指出了WGAN存在问题的原因,那就是WGAN在处理Lipschitz限制条件时直接采用了 weight clipping,就是每当更新完一次判别器的参数之后,就检查判别器的所有参数的绝对值有没有超过一个阈值,比如0.01,有的话就把这些参数 clip回 [-0.01, 0.01] 范围内。通过在训练过程中保证判别器的所有参数有界,就保证了判别器不能对两个略微不同的样本在判别上不会差异过大,从而 间接实现了Lipschitz限制。实际训练上判别器loss希望尽可能拉大真假样本的分数差,然而weight clipping独立地限制每一个网络参数的取值范围,在 这种情况下最优的策略就是尽可能让所有参数走极端,要么取最大值(如0.01)要么取最小值(如-0.01),文章通过实验验证了猜测如下图所示判别器的参 数几乎都集中在最大值和最小值上。
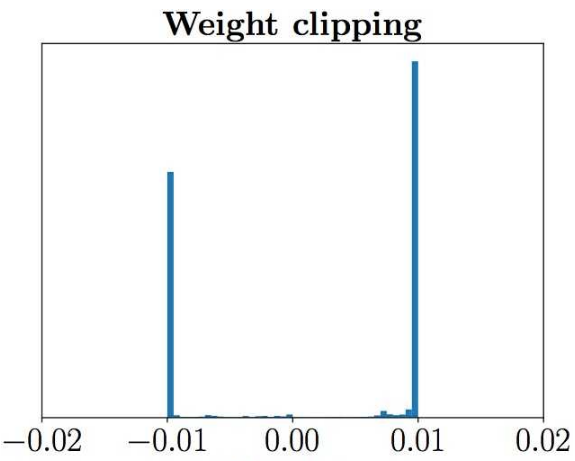
还有就是weight clipping会导致很容易一不小心就梯度消失或者梯度爆炸。原因是判别器是一个多层网络,如果把clipping threshold设得稍微小了一 点,每经过一层网络,梯度就变小一点点,多层之后就会指数衰减;反之,如果设得稍微大了一点,每经过一层网络,梯度变大一点点,多层之后就会指数爆 炸。只有设得不大不小,才能让生成器获得恰到好处的回传梯度,然而在实际应用中这个平衡区域可能很狭窄,就会给调参工作带来麻烦。文章也通过实验展 示了这个问题,下图中横轴代表判别器从低到高第几层,纵轴代表梯度回传到这一层之后的尺度大小(注意纵轴是对数刻度)
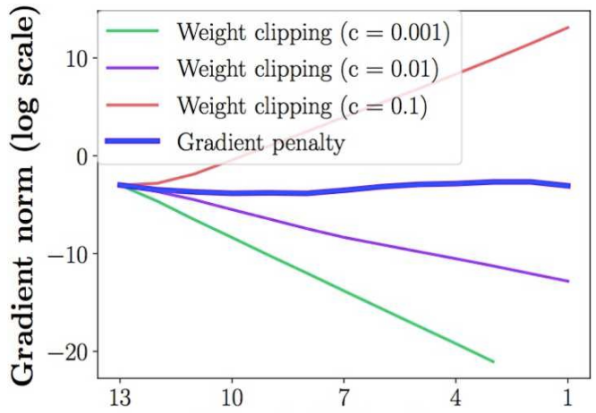
在以上问题提出后,作者提出了解决方案,那就是gradient penalty我翻译为梯度惩罚。Lipschitz限制是要求判别器的梯度不超过K,gradient penalty 就是设置一个额外的loss项来实现梯度与K之间的联系,这就是gradient penalty的核心所在,下图为引入gradient penalty后WGAN-GP的算法框图,对 于算法的分析我在附录中加以说明。

gradient penalty的选取并不是在全网络下,仅仅是在真假分布之间抽样处理,下图为处理过程。
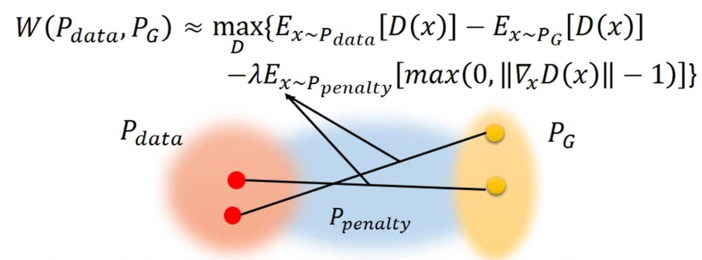
下面公式展示为WGAN-GP的最终目标函数:
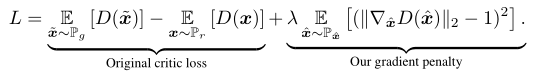
WGAN-GP的创新点也就在目标函数的第二项上,由于模型是对每个样本独立地施加梯度惩罚,所以判别器的模型架构中不能使用Batch Normalization, 因为它会引入同个batch中不同样本的相互依赖关系。
小结:WGAN-GP指出了WGAN存在的两大问题,weight clipping导致的参数集中化和调参上的梯度爆炸和梯度消失问题,改进的gradient penalty解决 了问题将参数与限制联系起来达到真实的Lipschitz限制条件。但是理论归理论实际实验上WGAN-GP的效果并不尽如人意,实验结果还没有WGAN的效果好, 我感觉问题应该是出在了gradient penalty上,但是具体的证明我还没到功夫,以后有时间好好研读推导一下。以下是附录部分,大家可选择性参考。
附录

谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/04/09/wgan-gp/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


