本文是关于《DEFORM-GAN:AN UNSUPERVISED LEARNING MODEL FOR DEFORMABLE REGISTRATION》论文的阅读笔记。
一、简介
文章提出了一种基于 GAN 的三维医学图像跨模态配准模型 Deform-GAN,并首次将梯度损失(gradient loss)应用到基于深度学习的配准模型中。模型是无监督的,不需要任何 ground-truth 或人工标注信息。
基于无监督的学习模型存在着两个挑战,一个是跨模态或跨序列配准中损失函数的确定,另一个是没有 ground-truth,这使得 GAN 模型比较难训练。
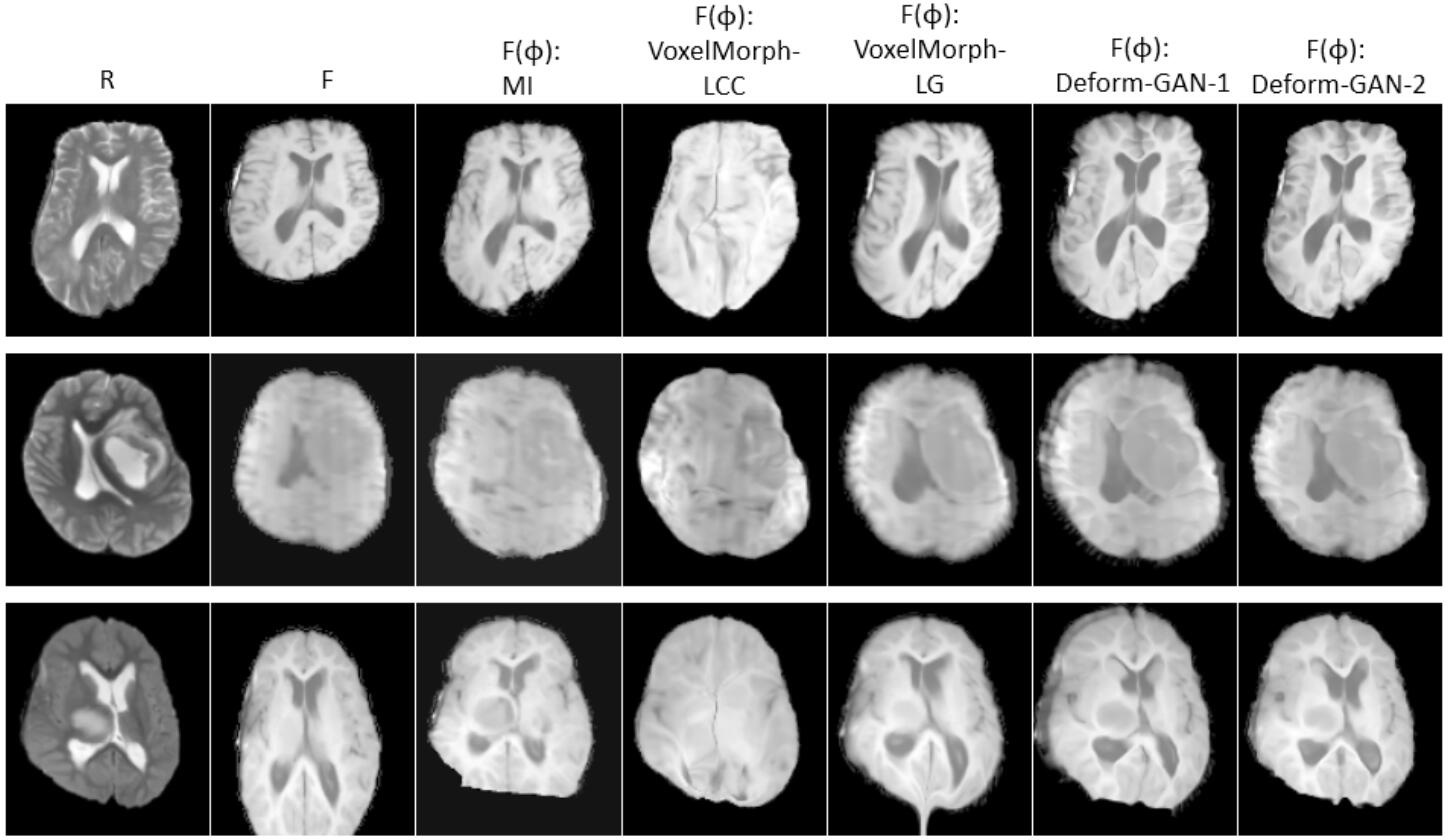
上图是 Deform-GAN 和其他模型的配准结果对比图。
二、记号
- $T$:图像变换网络
- $G$:图像生成器
- $D$:判别器
- $R$:参考图像
- $F$:浮动图像
- $\phi$:配准形变场
- $F(\phi)$:变形后的浮动图像
- $p$:体素位置
- $I$:三维图像
三、网络结构和训练
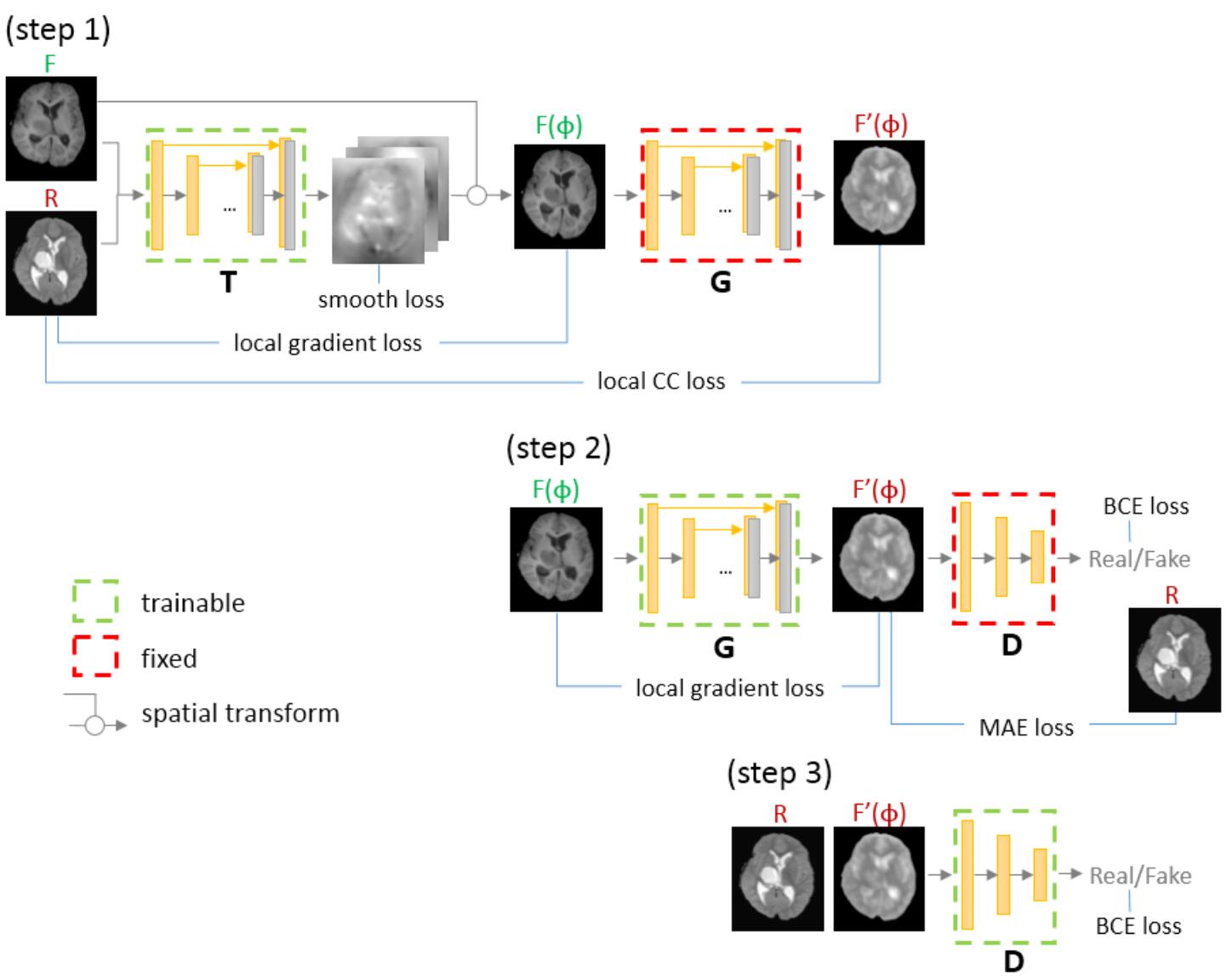
上图是 Deform-GAN 网络的结构示意图。
网络主要由三部分组成:图像变换网络 $T$,图像生成器 $G$ 和判别器 $D$,前两者采用的都是类似于 U-Net 的网络结构。图像变换网络 $T$ 的输入是参考图像和浮动图像的图像对,输出是配准形变场 $\phi$,$\phi$ 会进一步通过空间变换器对浮动图像 $T$ 做变形得到 $F(\phi)$,这一步相当于实现了模态间配准(从源域到源域)。图像生成器 $G$ 以 $F(\phi)$ 为输入,其输出是一个接近于参考图像 $R$ 的图像 $F’(\phi)$,这一步相当于实现了跨模态配准(从源域到目标域)。判别器 $D$ 用来判别图像是真实图像还是合成图像。如此一来,配准问题就被分成了两部分:多模配准和单模配准。
在训练前期,$T$ 还没有学习到很好的特征,配准效果不好,如果直接将 $R$ 和 $F’(\phi)$ (这里论文中写的是 $F(\phi)$,我怀疑是写错了,按照示网络结构示意图中的来)输入到判别器则会产生错误对齐的 $F’(\phi)$。为解决该问题,文章提出了“梯度约束的 GAN 方法”,这种方法的特点是损失函数不是固定的,而是通过学习获得的,它不仅惩罚输出图像和目标域图像之间的差别,而惩罚输出图像和源域图像之间的差别。
生成器的任务有三个:一是骗过判别器,二是最小化输出图像和目标域图像的 $L_1$ 距离,三是保持输出图像和源域图像在细节上保持相似。
在训练时,三个网络的训练顺序是先训练判别器 $D$,再训练生成器 $G$,最后训练图像变换网络 $T$,当训练一个网络时,其他网络的参数保持不变。
四、损失函数
局部梯度计算公式:
$$
\nabla \hat{I}(p)=\left(\sum_{p \in n^{3}} x^{\prime}(p), \sum_{p \in n^{3}} y^{\prime}(p), \sum_{p \in n^{3}} z^{\prime}(p)\right)
$$
$n$ 是 $p$ 周围的像素点个数,当 $n$ 较小时网络难收敛,当较大时图像 $R$ 和 $F$ 的边缘很难准确对齐,通过尝试当 $n=7$ 时效果最好。根据以上梯度的计算公式就可以得到正则化的梯度了:
$$
n(I, p)=\frac{\nabla \hat{I}(p)}{|\nabla \hat{I}(p)|+\varepsilon}
$$
其中 $||\cdot||$ 表示 $L_2$ 距离,图像 $R$ 和 $F$ 之间的局部梯度损失就可以定义为:
$$
L_{L G}(R, F)=\sum_{p \in \Omega}|n(R, p) \cdot n(F, p)|
$$
其中 $\Omega$ 是 $R$ 和 $F$ 的图像域,
图像转换网络 $T$ 的损失可以表示为:
$$
L_{T}(R, F, \phi)=L_{s i m}(R, F(\phi))+\alpha L_{s m o o t h}(\phi)
$$
其中 $L_{sim}(R,F(\phi))$ 又由两部分组成:图像 $R$ 和 $F’(\phi)$ 之间负的局部互信息和图像 $R$ 和 $F(\phi)$ 之间负的局部梯度距离,如下式所示:
$$
L_{s i m}(R, F(\phi))=-L_{L C C}\left(R, F^{\prime}(\phi)\right)-\beta L_{L G}(R, F(\phi))
$$
形变场的平滑损失 $L_{smooth}(\phi)$ 可以表示为:
$$
L_{\text {smooth}}(\phi)=\sum_{p \in \Omega}|\nabla \phi(p)|^{2}
$$
下面来看下生成器 $G$ 和判别器 $D$ 的损失函数。在 Pix2Pix 网络,它的损失函数为:
$$
L_{G^{*}}=\arg \min {G} \max _{D} L{c^{G A N}}(G, D)+\lambda L_{L 1}(G)
$$
其中 $L_{cGAN}$ 是条件 GAN(conditional GAN)的目标函数,$L_{L1}$ 是源图像和 ground-truth 的目标图像之间的 $L_1$ 距离。但是在本论文中由于源图像和目标图像不是像素级的映射数据,所以不适用。本文用局部梯度损失来限制合成图像 $F’(\phi)$ 和源图像 $F(\phi)$ 之间的梯度距离,并保证最终的输出图像的细节和源图像一致。所以最终 GAN 的总损失为:
$$
\begin{aligned}
L_{G^{\prime}}=& \arg \min {G} \max _{D} L{c^{G A N}}(G, D)-\mu L_{L G}\left(F^{\prime}(\phi), F(\phi)\right) \
&+\lambda L_{L 1}\left(F^{\prime}(\phi), R\right)
\end{aligned}
$$
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/04/05/deform-GAN/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


