本文是关于论文《CT Super-resolution GAN Constrained by the Identical, Residual, and Cycle Learning Ensemble (GAN-CIRCLE)》的阅读笔记,本来是想看有关cycle-GAN 的内容,但是错找成了 GAN-Circle 的论文。
一、研究背景
GAN-Circle 是一个半监督的深度学习网络,用来从低分辨率的 CT 图像生成高分辨率的 CT 图像。在模型中使用了 GAN、CNN、残差学习、网中网等技术。
对于当前的 CT 成像技术来说,虽然分辨率已经很高了,但是在早期肿瘤描绘和冠状动脉分析等方面分辨率仍然不够。所以如何在使用低辐射剂量的前提下产生出高分辨率的图像是一个热门的问题。一般来说有两种思路,一种是硬件定向的方法,如提高 CT 成像设备的精度等,但这种方法往往很昂贵,并且可能产生较高的辐射;另一种是软件计算的方法,主要的挑战是对低像素图像去模糊。
对于软件计算的提高 CT 分辨率的方法,主要有三类方法:
- 第一种是基于模型的重建方法,它可以通过对图像的退化过程进行建模并且对重建过程进行了正则化;
- 第二种方法是基于学习的方法(可理解为基于机器学习的方法),它是从训练数据中学习一个从低分辨率图像到高分辨率图像的非线性映射,从而来恢复低分辨率图像所丢失的高频信息;
- 第三种是基于深度学习的方法,和第二种类似,但是使用的是深度学习,这也是近来最热门的方法。
基于深度学习的方法有几个局限:
- 基于深度学习的有监督的模型需要低分辨率图像和与其匹配的高分辨率图像来进行训练,而这些图像是比较少且难获得的,所以只能诉诸于半监督的方式;
- 使用 GAN 时,网络可能产生目标图像中未显示的特征。GAN 网络从输入图像 $x$ 产生输出图像 $\hat{y}$,但是它不能确定两者是否是匹配的,因为可能有多种不同的输入能够产生相同的输出,这就会产生模型崩溃问题,为解决该问题使用了具有循环一致性(Cycle-consistent)的 GAN;
- GAN 的学习过程不好控制;
- 当网络的层数增加时,参数随之增加,训练所需的内存和时间开支很大;
- CT 图像的局部特征有不同的尺度;
- 预测的高分辨率图像 $\hat{y}$ 和真实的高分辨率图像 $y$ 之间的 $L_2$ 距离经常被用作损失函数,但是可能会产生过度光滑的问题,因为 $L_2$ 距离意味着最大化峰值信噪比(PSNR)。
二、记号
- LR——低分辨率(low resolution)
- HR——高分辨率(high resolution)
- SR——超分辨率(super resolution)
- X——源域
- Y——目标域
- x——源域中的图像(LR 图像)
- y——目标域中的图像(HR 图像)
- $\hat{x}$——生成的假的 LR 图像
- $\hat{y}$——生成的假的 HR 图像
- G——将 LR 图像转化为 HR 图像的生成器
- F——将 HR 图像转化为 LR 图像的生成器
- $D_Y$——判别生成的 HR 图像与真实图像是否相似的判别器
- $D_X$——判别生成的 LR 图像与真实图像是否相似的判别器
三、深度循环一致性对抗模型
本文的主要贡献有:
- 提出了一种新颖的 CycleGAN 框架下的基于 CNN 的残差网络,具体的使用了循环一致性来增强源域与目标域之间的跨域一致性;
- 在训练时使用 Wasserstein 距离或 Earth Moving(EM)距离来代替 Jensen-Shannon(JS)距离来解决 GAN 网络训练中的问题;
- 根据几个基本的设计原则来优化网络,从而避免过拟合和降低计算开销;
- 级联了多层来学习特征;
- 使用跳跃连接来避免梯度消失;
- 使用 $L_1$ 正则代替 $L_2$ 正则来优化去噪。
在恢复高分辨率 CT 图像时的主要挑战有:
- 与自然图像相比,低分辨率 CT 图像有着不同的或者更复杂的空间变化、相关性和统计特性;
- 低分辨率图像中的噪声可能在重建过程中产生影响;
- 由于采样和降质操作是耦合的、不适定的,传统的方法不是很适用。
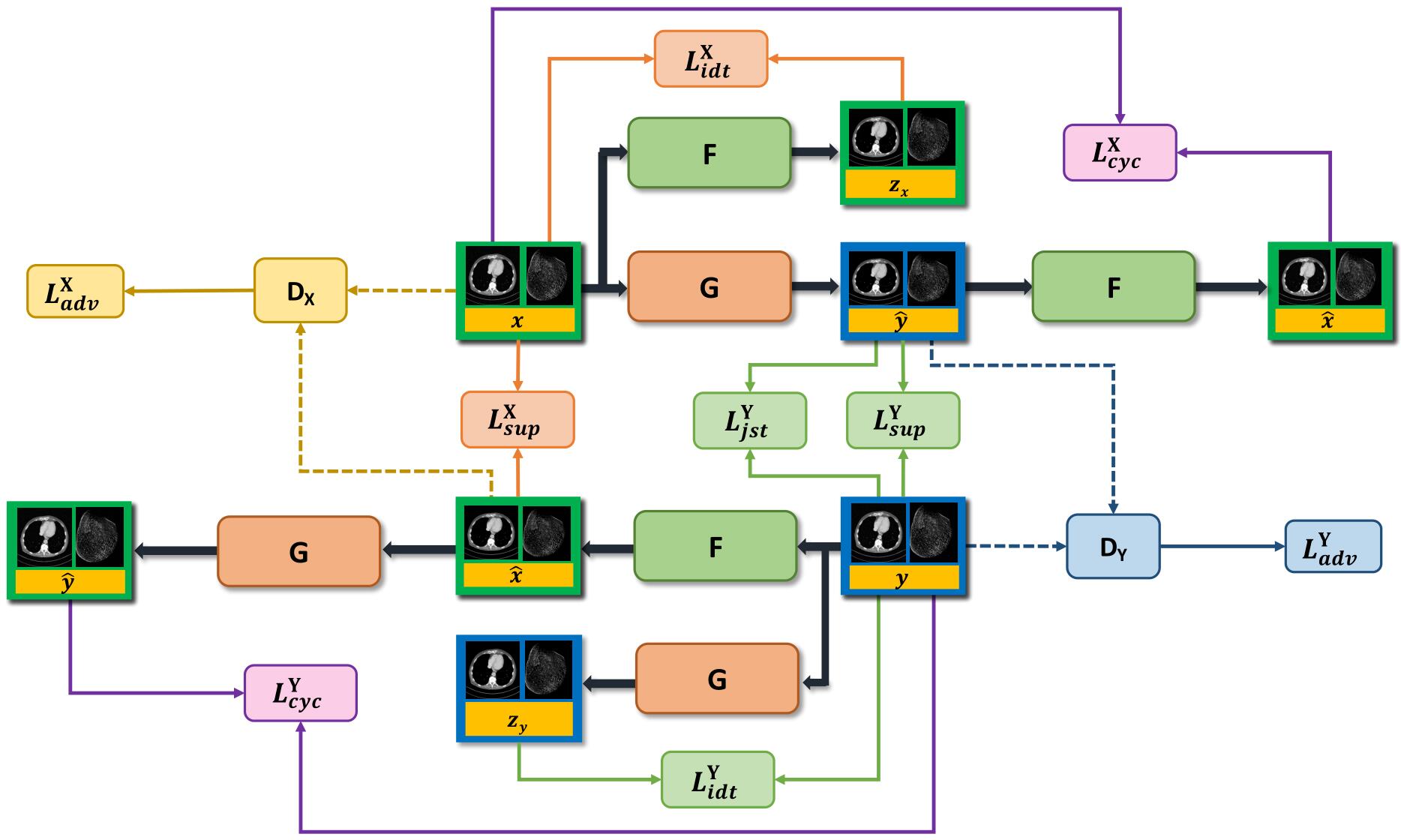
上图是循环一致性模型的结构示意图,可以分为上下两部分,这两部分是对称的,标有 x、y 的块是输入图像,绿色块是低分辨率图像,蓝色块是高分辨率图像。
在该模型中一共有两个 GAN,它们的结构相同,功能不同,一个是从 LR 图像生成 HR 图像,然后做对抗学习;另一个是从 HR 图像生成 LR 图像,然后做对抗学习。两者之间也有一定的联系。这样我们优化的问题就变成了:
$$
\min_{G,F}\max_{D_Y,D_X}L_{GAN}(G,D_Y)+L_{GAN}(F,D_X)
$$
四、损失函数
在训练过程中一共有四种损失函数:对抗损失(adversarial loss, adv)、循环一致性损失(cycle-consistency loss, cyc)、一致性损失(identity loss, idt)和联合稀疏变换损失(joint sparsifying transform loss, jst)
对抗损失的作用是促使生成的图像遵循源域或目标域的分布,在具体使用的时候使用了 Wasserstein 距离来代替负的对数似然损失,其表达式为:
$$
\min_G\max_{D_Y}L_{WGAN}(D_Y,G)=-E_y[D(y)]+E_x[D(G(x))]
$$$$
+\lambda E_{\hat{y}}[(||\nabla yD(y)||_2-1)^2]
$$其中 E() 表示期望,y 表示对于 G(x) 和 y 的沿直线的均匀采样,$\lambda$ 是规范化参数。$\min_F\min_{D_X}L_{WGAN}(D_X,F)$ 的表达式也与上式类似。
循环一致性损失:研究证明单纯使用对抗损失不能很好的实现从源域到目标域图像的转换,所以又使用了循环一致性损失。简单来说,就是先把 LR 图像转换为 HR 图像,再转换回 LR 图像,然后将原始 LR 图像和结果计算损失函数,使得 $F(G(x))\approx x$ 。HR 图像同理。其表达式为:
$$
L_{CYC}(G,F)=E_x[||F(G(x))-x||_1]+E_y[||G(F(y))-y||_1]
$$一致性损失:相比于 $L_2$ 正则,$L_1$ 正则可以容忍估计图像和目标图像之间的小错误,并且收敛速度更快。
$$
L_{IDT}(G,F)=E_y[||G(y)-y||_1]+E_x[||F(x)-x||_1]
$$联合稀疏变换损失:为了表示图像稀疏性,我们在以下联合约束条件下建立了一个基于非线性全变分的损失函数,其表达式如下:
$$
L_{JST}(G)=\tau||G(x)||{TV}+(1-\tau)||y-G(x)||{TV}
$$
其中 $\tau$ 是比例因子,设置为 0.5。
总的损失函数为:
$$
L_{GAN-CIRCLE}=L_{WGAN}(D_Y,G)+L_{WGAN}(D_X,F)
$$
$$
+\lambda_1 L_{CYC}(G,F)+\lambda_2 L_{IDT}(G,F)+\lambda_3 L_{JST}(G)
$$
当有监督信息也就是成对的图像 (x,y) 时,还可以加入监督损失,其公式如下:
$$
L_{SUP}(G,F)=E_{(x,y)}[||G(x)-y||1]+E{(x,y)}[||F(y)-x||_1]
$$
五、网络结构
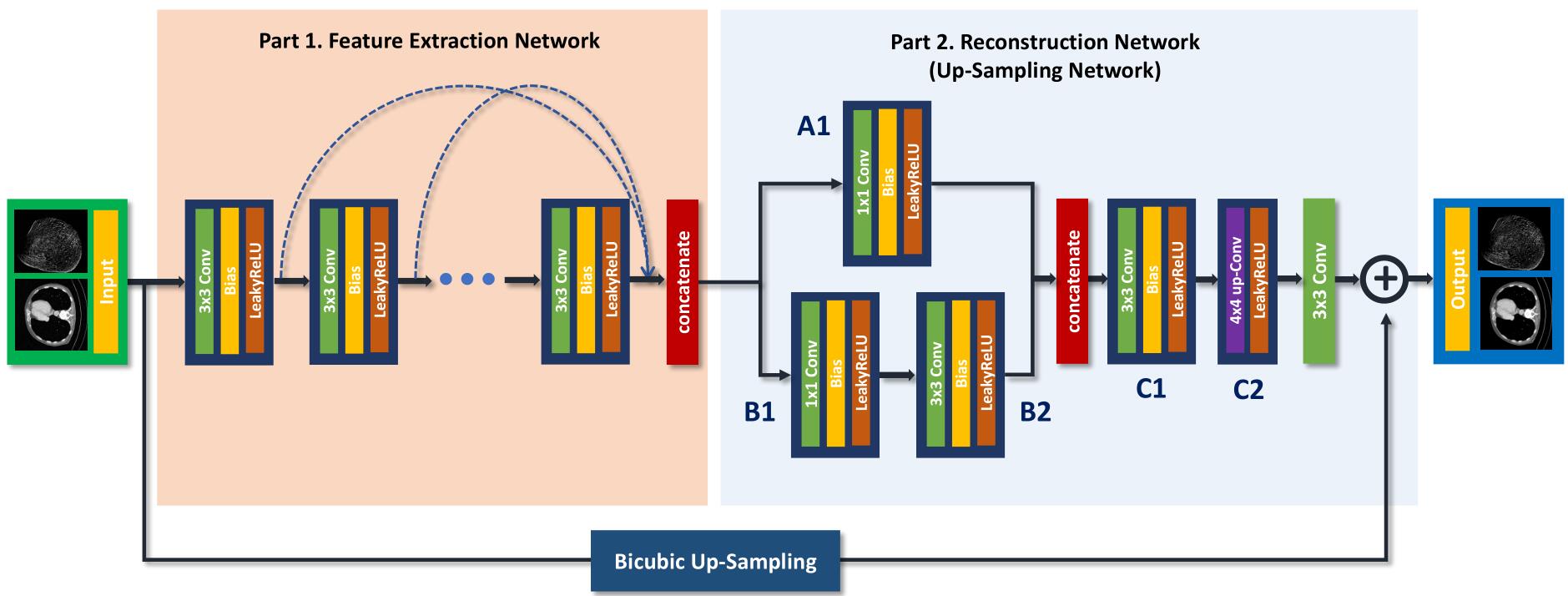
上图是生成网络的结构示意图,如图中所示, 生成网络包括特征提取网络和重建网络两部分,特征提取网络由12个非线性特征 SR 特征块组成,每个非线性 SR 特征块 $3\times3$ 的卷积、偏置和 Leaky ReLU 组成,为了提取局部和全局的图像特征,各个隐藏层的输出通过跳跃连接结合,如图中虚线所示。
在重建网络中有两个重建分支,在图中表示为 A、B 分支,然后将两个分支合并为 C。这种网络结构通过多个分支进行运算,然后再将其输出结果合并的结构被称作网中网(network in network),而在 GoogLeNet 中被称作 Inception Module。其中的 $1\times1$ 卷积有两个优点,一方面是过滤器较小,计算快,另一方面可以提升网络的非线性性,使其可以学到更复杂的映射关系。
当是有监督的训练时,生成网络中还对原图进行了双三次插值,然后与重建网络的输出结果进行合并得到最终的结果。

上图是判别网络的结构示意图,判别网络由8个块组成,每个块由 $4\times4$ 卷积、偏置、实例正则化和 Leaky ReLU 组成,后面跟着两个全连接。图中 n64s1 中的 n64 表示通道数,s1 表示步长为1。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/04/02/GAN-circle/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


