本文是关于论文 Nonrigid Image Registration Using Multi-scale 3D Convolutional Neural Networks 的笔记。
个人觉得本文主要有两个创新点,一个是 ground-truth 的获取方式,是通过对 moving image 变形来得到 fixed image 的;另一个是网络的结构采用了多尺度的输入,并且没有把两个不同大小的图像块拼接成一个双通道的输入(当然图像块大小不同也合并不了),而是分别对其做处理然后再合并。
在之前的方法中,如果某些数据和模型不匹配则会在配准时不会有很好的效果,这时通常会采取修改差异性度量的方式来解决。在这篇论文中不采用手工修改模型的方式,而是用机器学习的方式来自动决定。也就是不显式的定义差异性度量标准。
本文提出的模型叫做 RegNet(不得不说这名字真不咋地,毫无特点),它的输入是多尺度的图像块对,网络的输出是一句具有3个元素的向量,它表示图像块的中心像素的位移。文章声称这时第一个用端到端的 CNN 来解决 3D 非刚性图像配准的模型。
记号:fixed image 记为 $I_F$,moving image 记为 $I_M$,像素 $x$ 从 fixed image 到 moving image 的位移记为 $u(x)$,像素的变换记为 $T(x)=x+u(x)$
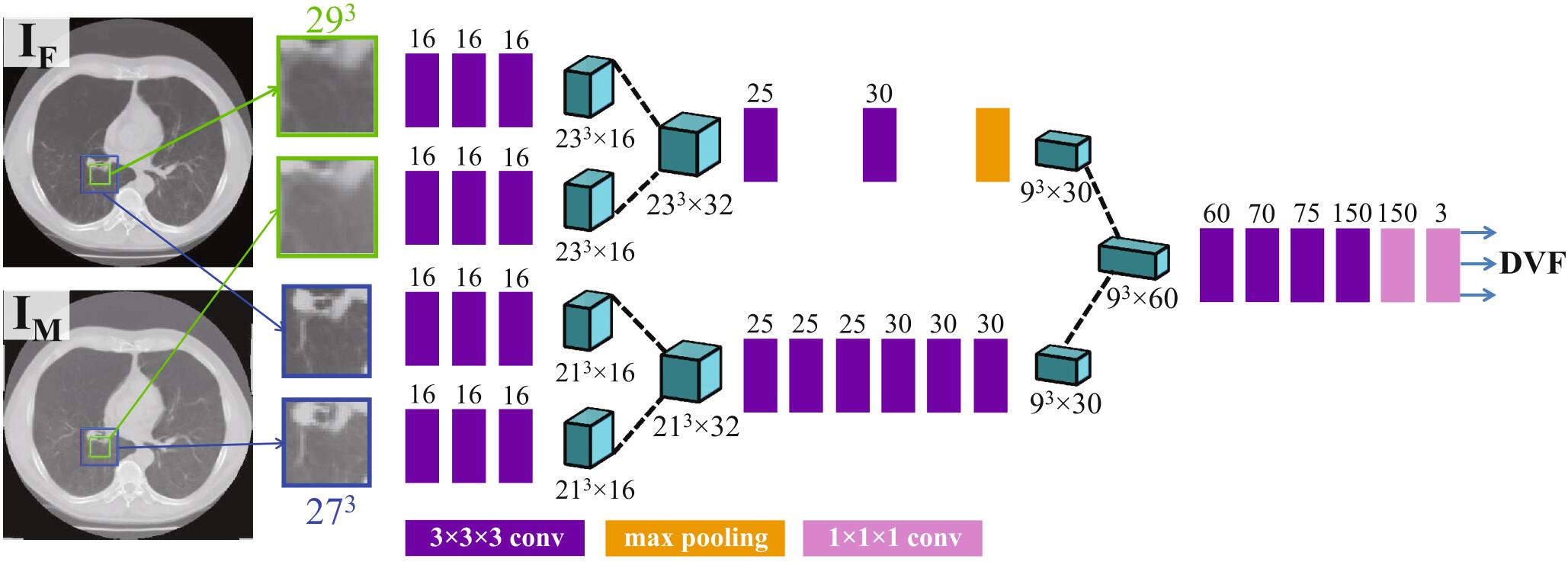
模型的结构如上图所示,每个图像块后面跟着3个卷积层,然后对于相同大小的来自 fixed image 和 moving image 的图像块进行拼接(第一个深绿色部分),然后分别经过2个卷积、一个最大池化和6个卷积操作,然后这两条不同的处理路径得到的结果也会进行拼接(第二个深绿色的部分),然后后面通过4个卷积操作和2个全连接操作最终得到输出——位移向量场 DVF。其中每个卷积层后面都跟着一个 ReLU 激活函数和 batch normalization 操作。
输入时的多尺度是指,一方面取原图的一个 $29\times29\times29$ 的图像块作为输入,另一方面先取原图的一个 $54\times54\times54$ 的图像块,再对其下采样为 $27\times27\times27$ 大小的图像块作为输入。这样分别对 fixed image 和 moving image 进行以上两种采样,然后就得到了4种不同大小(尺度)的输入,所以称之为多尺度输入。
优化器使用的是 Adam 优化器,并且采用衰减的学习率,学习率初始值为0.001,衰减因子为每个 epoch1.25。损失函数采用的是平均剩余距离(the mean residual distance),其公式为 $MAE=\frac{1}{n}\sum^n_{n=1}|DVF’_i-DVF_i|$。其中 $DVF_i’$ 是模型预测的 DVF,而 $DVF$ 是通过以下方式人工合成的。
通过不同的空间频率和幅度来人工合成 DVF,主要分为以下三个步骤:
- 创建一个和输入图像相同大小的向量场(它作为 moving image),并初始化为0
- 随机选取 DVF 中的 P 个带你,并随机给位移向量附取值范围为 $[-\theta,\theta]$ 的3个值
- 用标准差为 $\sigma$ 的高斯核对 DVF 进行平滑处理。
使用三组不同的设置 $\sigma=35、P=80、\theta=8$,$\sigma=25、P=100、\theta=8$,$\sigma=20、P=100、\theta=8$ 来分别生成低中高频的变形 DVF,然后对输入图像应用该 DVF 并采用三次 B 样条插值得到 fixed image。为了得到更真实的图像,最后还在图像中加入标准差为5的高斯噪声。
后面还有一段没读懂,直接把翻译结果放在这:对于单个运动图像,可以产生大量的变形,但是这种方法的缺点是运动图像在每对输入图像中是相同的,因为只有固定图像是随机生成的。因此,我们还生成运动图像的变形版本,并基于此创建新的变形图像。新的运动图像仅使用低频变形生成,以避免过度拉伸(导致外观模糊)。在这一步中,我们使用设置 $\sigma=35、P=100、\theta=8$ 和标准偏差为3的高斯噪声。
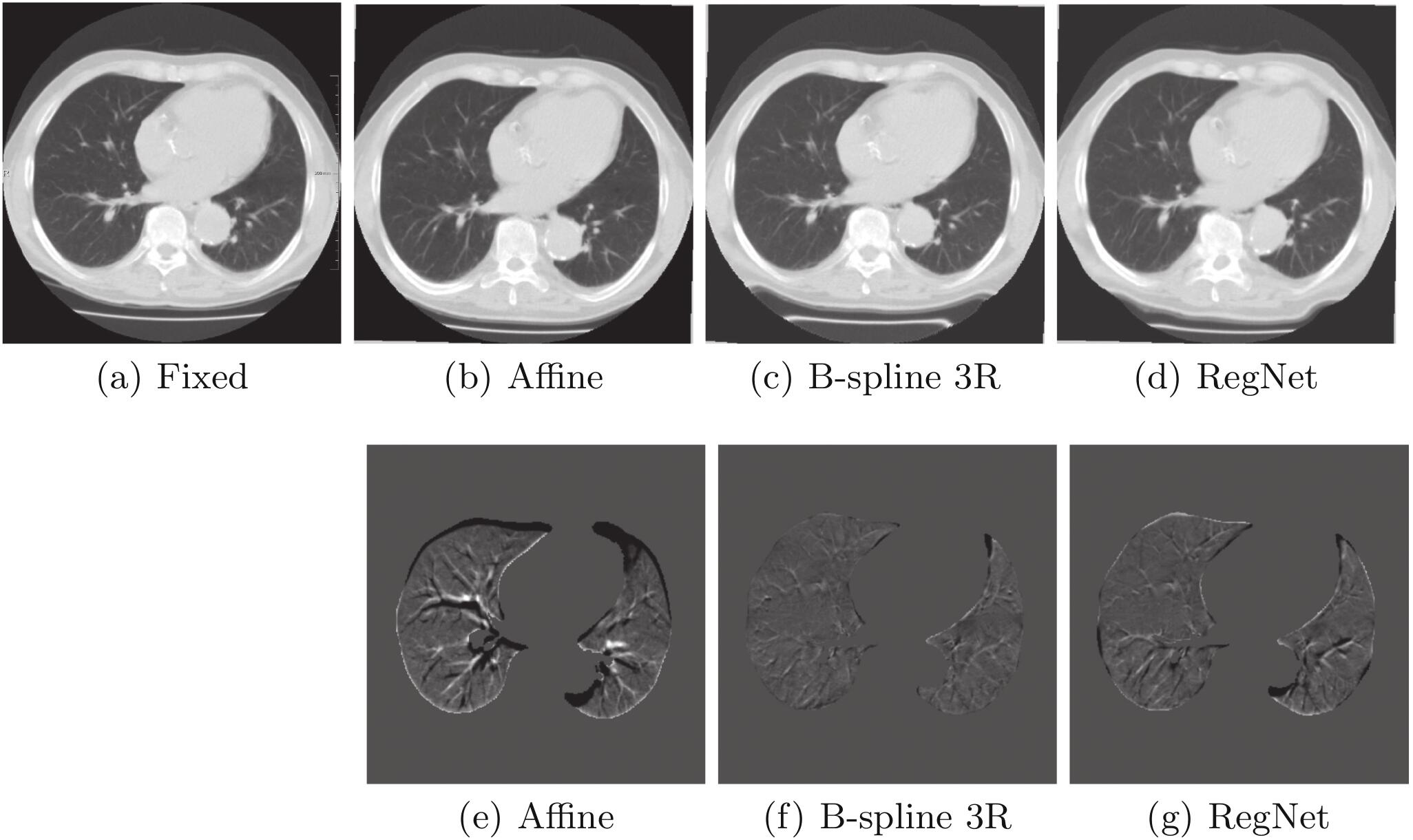
从不同模型的结果对比图来看,RegNet 的结果还是不错的,但是比 B-spline 3R 还是差一点。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/03/13/RegNet/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


