本文是递归级联网络和 VTN 网络论文,及其代码的一些解读。
一、递归级联网络
递归级联网络论文地址:递归级联网络论文
1. 前人工作
之前的工作尝试通过对一些现有网络进行堆叠来建模的,但是每一层网络的输入和任务各不相同,并且是对每一层依次单独训练的(先训练之前的层,将之前层的参数固定下来后再训练后面的层),每一层都会计算 warped image 和 fixed image 之间的相似性损失,这导致了当堆叠到很少层(大约3层)之后,实际效果就不再有任何提升了。
这是因为复杂变形场一般有着较大的位移,所以网络直接预测复杂的形变场不易实现,同时逐层训练的网络结构中,每一层都是各学各的,所以无论怎么级联,都很难达到很好的效果。
2.递归级联网络
递归级联网络是一个端到端的无监督模型,理论上它可以基于任意网络来做,当模型的级联的层数越多时,模型的效果越好。

上图是用递归级联网络对肝脏 CT 数据进行配准的示意图,moving image 通过每一层后不断的产生扭曲,最终对齐到 fixed image。图中的 $\phi_k$ 表示一个预测流场(predicted flow field)。
对于递归级联网络中“递归”和“级联”的含义,我的个人理解是,级联就是把多个子网络串联起来形成一个级联块,这些子网络可相同,也可不同。而递归就是把级联块重复的使用多次,并且所有级联块具有相同的参数。

上图是递归级联网络的结构示意图。
递归级联网络的每一层的输入都是经过前几层处理后的图像(warped image)和固定图像(fixed image),并且舍弃了逐层训练的方式,而是采用联合训练的方式,只在最后一层来计算 warped image 和 fixed image 之间的相似度,通过反向传播更新前面的所有层。这样一来,每一层只需要学习简单的变形场,所有层级联之后就达到很好的效果。
文章中递归级联网络所使用的基础网络是 VTN 和 VoxelMorph,前者占用的显存更少。文章建议在级联时第一个网络是仿射网络(affine network),也就是级联时第一个网络为仿射网络,后面跟着若干其他子网络。
每个子网络会根据输入的 fixed image 和 warped image 来预测一个变形流场(deformable flow field),每一层的子网络可以相同,也可以不同,方便起见一般会选择相同的子网络。
图像重采样使用的是(多)线性插值,在超出原图边界的采样点上使用最近点插值。
参数共享级联,即递归。本文提出的递归结构有两种形式,即假设一共有 $n$ 个级联块,第一种递归形式是把这 $n$ 个级联块重复使用两次,因此就得到了 $2n$ 个级联块。第二种递归形式是把每个级联块就地使用 $r$ 次,那么就得到了 $rn$ 个级联块。举例来说,比如级联块是 ABCD,若重复三次,则第一种方式的结果为 ABCDABCDABCD,第二种的结果为 AAABBBCCCDDD。后者的效果更好。训练的时候为了节省显存开支没有使用递归,在测试的时候才用。
二、VTN
VTN 论文地址:VTN 论文
VTN 是 Volume Tweening Network 的缩写,其论文发表时间和递归级联网络几乎一致,给我的感觉是作者做了一次实验,发了两篇论文。VTN 论文中没有单独给出 VTN 网络的代码,而是给出了递归级联网络的 github 地址(见第三部分)。
VTN 是一种基于无监督的学习方法的端对端网络框架,用来进行 3D 医学图像的配准。有三个创新点:
- 端对端的级联方案,这是为了解决大尺度变形的问题
- 有效的结合了仿射配准网络
- 使用一个额外的可逆性损失(invertibility loss)来鼓励后向一致性(backward consistency)
VTN 网络是在光流估计(Optical flow estimation)和 STN(Spatial Transformer Networks) 的基础上做的,前者是为了识别在同一场景不同角度的两张图片中像素点之间的相关性;后者是为了学习一个定位网络来产生一个合适的变换以拉直输入图片。

上图是 VTN 级联的示意图,其中配准子网络用来寻找 fixed image 和当前 moving image 之间的变形场,fixed image 还会和当前 moving image 产生一个相似性损失来指导训练,有颜色的实线表示损失是怎么计算的,有颜色的虚线表示梯度是怎么反向传播的,因为每一层都可微,所以当前层产生的梯度可以传播到之前的所有层。
VTN 是由多个子网络级联而成的,每个级联的子网络可以产生一个变换来让 moving image 和 fixed image 对齐。当前层只根据前一层的输出(warped image)和 fixed image 来产生变换(transform),而前人所提出的网络除了上述两个输入,还要输入最初的 moving image。这种级联子网络的想法来自于 FlowNet 2.0。VTN 网络的结构包括仿射(affine)配准和可变形(deformable)配准两个过程,一般是一个仿射配准网络,后面跟多个可变形配准网络。此外还加入了可逆性损失来鼓励后向一致性,以达到更高的精度。

上图是仿射配准网络的示意图,其中四边形上方是通道数,四边形越大表示分辨率越高。
仿射配准子网络用仿射变换来对齐输入图像(fixed image and moving image),它只被用作第一个子网络。仿射配准网络的卷积部分和下面的密度可变形网络的编码器部分是一模一样的,在一系列卷积操作后是一个全连接层,以形成一个仿射流场,即一个 $3\times3$ 的转换矩阵 A 和一个 3 维的位移向量 b。应该是对应旋转和平移操作中的参数。

上图是密度可变形网络的示意图,其中从卷积到反卷积的连线即跳跃连接。
密度可变形(dense deformable)配准子网络用作所有的后续子网络,其目的是让配准更加完善,它采用编码器-解码器结构,并且使用跳跃连接,该子网络会输出一个密度流场(dense flow field)和一个3通道的体积特征图(volume feature map)。
就递归级联网络和 VTN 网络的论文来看,两者的表述是有点矛盾的;从递归级联网络的代码来看,VTN 网络指的只是上述中的密度可变形网络,而递归级联网络则是一个仿射配准网络后面跟上多个 VTN 网络(密度可变形网络)。此外,递归级联网络的论文中说只有在最后一层才计算 warped image 和 fixed image 之间的相似性损失,而在 VTN 的论文中(VTN 的网络示意图中),是每层都计算相似性损失的。
三、代码
递归级联网络代码的github地址:递归级联网络
代码中文件的调用结构如下:

VTN 网络的结构:

VTNAffineStem 网络的结构和 VTN 网络中前半部分的卷积(conv1~conv6_1)相同,在此之后是一个全连接层将输出转化为一个 $3\times 3$ 的转换矩阵 A 和一个 3 维的位移向量 b。
在 VTNAffineStem 的代码中,除了一系列卷积和全连接操作之后,还有一些代码,数学系的师兄说其作用是正交约束,师兄给出的推导过程如下:
假设 $A^2=C=[c_{ij}]$ 具有三个特征值 $k_1,k_2,k_3$,希望它们均接近 1 等价于最小化下式:
$$
k_1+\frac{1}{k_1}+k_2+\frac{1}{k_2}+k_3+\frac{1}{k_3}=(k_1+k_2+k_3)+(\frac{k_2k_3+k_1k_3+k_1k_2}{k_1k_2k_3})
$$
$C$ 的特征多项式为(一次项前面的系数是所有可能的二阶主子式的和):
$$
p(k)=|C|-\sum_{1\leq i< j\leq3}(c_{ii}c_{jj}-c_{ij}c_{ji}k+tr(C)k^2-k^3)
$$
其中 $tr$ 是 $C$ 的迹,利用特征多项式根与系数的关系可得:
$$
k_1+k_2+k_3=tr(C)=c_{11}+c_{22}+c_{33}=\sigma_1
$$
$$
k_2k_3+k_1k_3+k_1k_2=\sum_{1\leq i<j\leq3}(c_{ii}c_{jj}-c_{ij}c_{ji}=\sigma_2)
$$
$$
k_1k_2k_3=|C|=\sigma_3
$$
所有待优化的目标函数变为:
$$
\sigma_1+\frac{\sigma_2}{\sigma_3}
$$
这个函数的最小值为 6,代码中减去 6 是为了让最小值成为 0。
2020.0809更新
四、实验
基础网络可以是VTN或者VoxelMorph,前者最多可以级联10次,后者最多可以级联5次。在肝脏CT图像和脑部MRI图像上做了实验。在CT数据集上是从数据集中随便拿两张图片做配准,而在MRI数据集上是将其他图片配准到一个固定的图谱(atlas)。选用的肝脏CT数据集有:MSD、BFH、SLIVER、LiTS、LSPIG,脑部MRI数据集有:ADNI、ABIDE、ADHD、LPBA,LPBA数据集用作测试,其他用作训练。
在VTN中相关系数被用作相似度度量标准,batch size设为4,需要迭代训练10w次,选用Adam优化器,初始学习率为$10^{-4}$,之后经过$6\times10^4$次迭代减半,再经过$8\times10^4$次迭代减半。
选用的baseline为VTN、VoxelMorph以及SyN、Elastix B-spline模型。使用Dice值来衡量模型的效果,其公式如下:
$$
\operatorname{Dice}(A, B)=2 \cdot \frac{|A \cap B|}{|A|+|B|}
$$
此外在某些数据集中是有地标标注信息的,所以可以将配准后地标点的平均距离作为额外的衡量标准。
在预处理阶段,先将所有图像中不必要的部分裁掉,然后重采样到$128\times128\times128$大小。脑部MRI图像还需要先用FreeSurfer去除头骨。
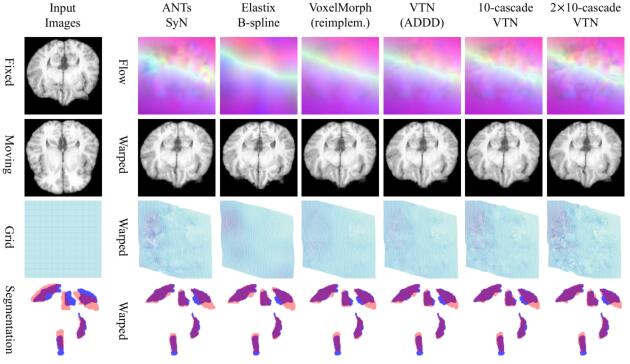
上图展示了在LPBA数据集上配准结果,第四行的分割中一共有5个解剖结构,蓝色代表固定图像的分割,红色的代表配准后图像的分割。
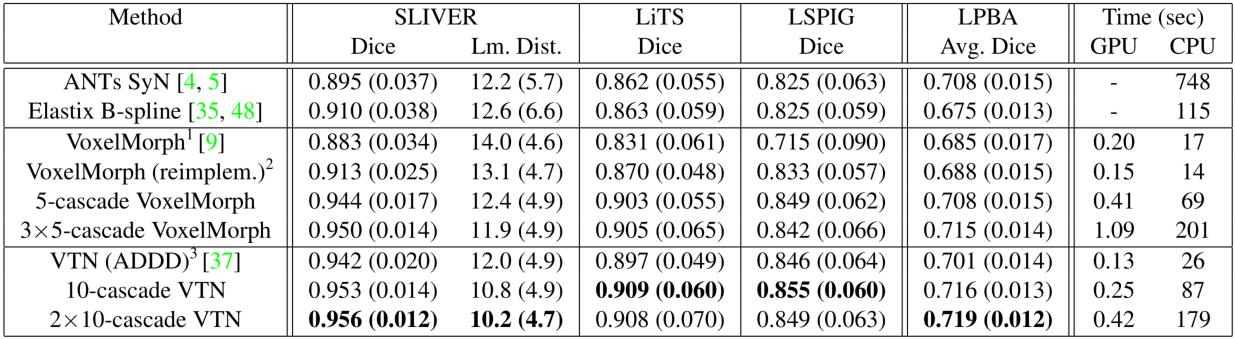
从上表1可以发现,递归级联网络的效果超过了其他的模型,并且其效果不受基础网络的限制。
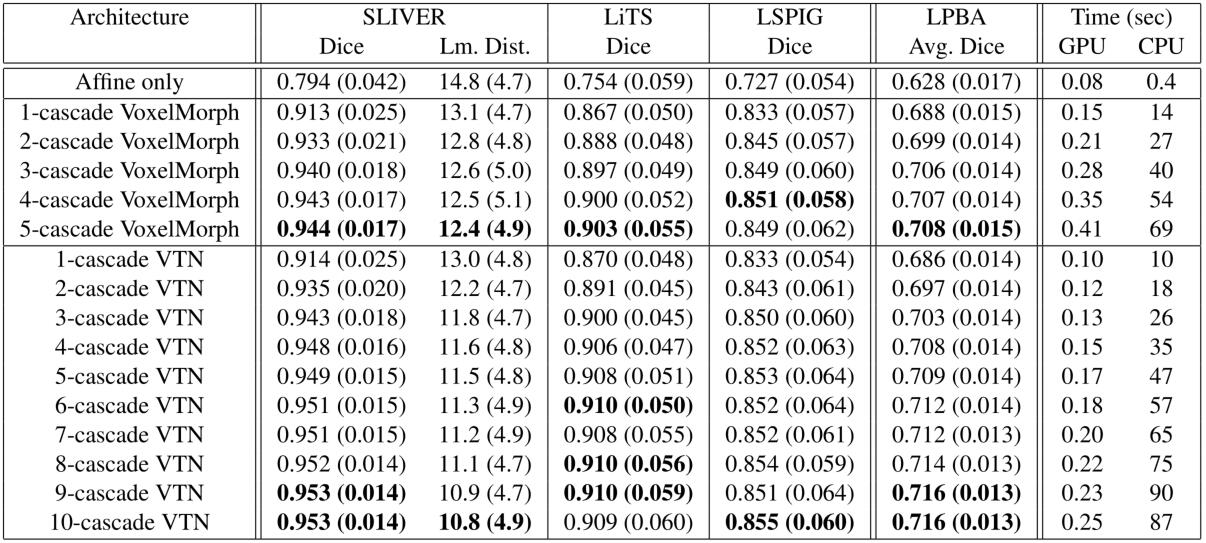
上表展示了当级联次数不同时,模型的表现,可以发现当VTN级联3次时,已经超过了表1中的VTN(ADDD) 模型了。当级联越多时,进行配准需要的时间也会线性增加。
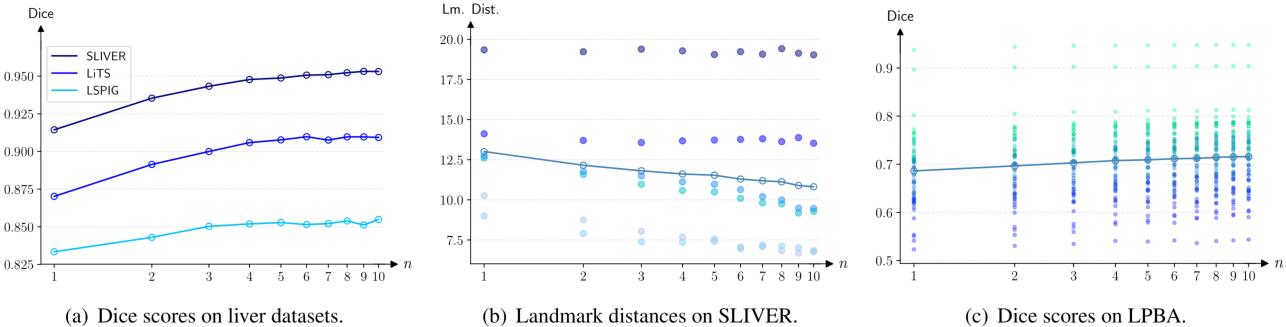
上图中横坐标是级联次数,纵坐标是效果,可以发现当级联次数越多时,效果是逐渐提升的。
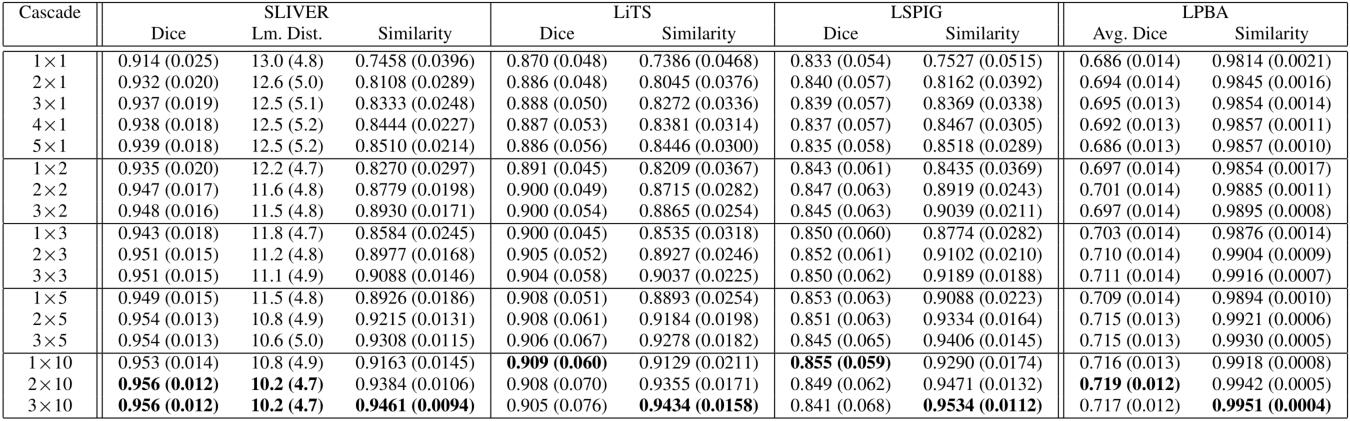
由于级联块的参数是共享的,所以可以级联到很深,上图中$2\times5$之类的就表示有5个参数共享的级联块,重复了2次。
此外还将VoxelMorph的通道数double进行了实验,发现效果有提升,但是不如递归级联网络,并且参数量变为了原来的4倍。
- 本文作者: 俎志昂
- 本文链接: zuzhiang.cn/2020/02/11/RCN/
- 版权声明: 本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议。转载请注明出处!


